- Get link
- X
- Other Apps
Featured Post
- Get link
- X
- Other Apps
#39WBE_Scaling_Law_上
/*-------------分隔線-------------*/
在本站我們討論過非常多指數律,舉凡貓喝水、動物的移行、吸花蜜、腫瘤代謝、動物甩水、游泳等等,相信讀者們對於指數律常用的分析方法都有一些基本的認識。在連續約兩三周左右的時間,我們要來深入探討生物學現象的指數律中最最最重要的一篇文章:
West, G. B.,
Brown, J. H., Enquist, B. J. (1997). A general model for the origin of
allometric scaling laws in biology. Science
276: 122-126.
這篇文章的引用次數超過三千次。我們要來深入討論他。
/*-------------分隔線-------------*/
生物的一些重要參數如心跳速率、呼吸速率、代謝速率等等與生物體質量之間的指數律,早在1892年就已經被發現,我們觀測到的exponent都非常接近我們熟悉的分數如1/4, 3/4, 1/2,
1等等,這強烈暗示背後有一個明確的物理機轉可以解釋這個現象,但是100年過去,雖然間間斷斷有些理論可以個別解釋一部份的現象(向我們討論過1974年McMahon利用elastic
similarity解釋走路和跑步與質量的關係),一直缺乏一個集大成的理論解釋生物體各種面向與質量之間的scaling law。
G. B. West因此思考,前人觀測的現象如主動脈半徑、心跳速率、肺臟體積、心輸出量等等,這些器官或現象存在的共同目的就是─要讓營養送到該送的地方,要把該帶走的廢物帶走,簡單的說就是和物質運送有關係。所以說如果我們能概念性的描繪出這個物質運送的網路,利用我們熟知的流體力學理論,我們就應該可以計算出這個網路在運送過程中耗損的能量。因此要讓理論模型繼續走下去的唯一方法就是─描繪出物質運送的網路。
描繪出網路當然需要一些假設。以氣管為例,氣管會分支成左右兩個主支氣管,再分支成5個支氣管,再分支成20個分截支氣管、…,這樣不斷分岔直到變成肺泡,填滿整個肺臟的現象,他認為可以用碎形(fractal)來模擬。第二個假設是,網路的最小單位(如微血管)「『對於不同生物而言』」是固定的尺寸(例如微血管的直徑約為7~8μm)。最後也是最重要的假設是,最後的網路是能最小化運輸成本的網路,也就是最小化能量耗損的網路。
注意到以下的討論並不完全符合生物體真實的情況,但這是讓討論能夠繼續的方式。你可以把這當成是個必要之惡。
現在大概基本的參數都定義好了,但是有個問題是,我們還沒有把第k階的參數和第k+1階的參數間的關係找出來。如果我們能找到的話,我們就能利用遞迴關係輕鬆描述整個網路。
(以下描述順序與原文章差異甚大,但小編認為這是比較符合邏輯的方式。)
我們假設管路的分支數目為碎形,即每級的分支給出的次級分支都是固定的數值n。在這裡我們先把會用到的一些東西定義先寫出來,之後我們會再利用Lagrange
multiplier證明這個系統除了管路數目以外的其他性質也必須遵從碎形。為了方便描述遞迴關係,我們定義βk= rk+1
/ rk,γk= lk+1 / lk。假設全身上下血管都是同時充血(注意這其實不正確,因為有precapillary
sphincter),則血液總體積為:
再來因為我們要知道的是整個網路系統的消耗功率,功率等於流量平方乘上阻力(可以想像成國中學過的P=I2R)。假設血流遵從Poiseuille flow,我們已經推導過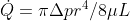 ,所以第k級血管的阻力當然就可以寫成
,所以第k級血管的阻力當然就可以寫成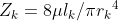 。而整個血管系統的總阻力就可以寫成(其實就是串並聯的電阻而已 ):
。而整個血管系統的總阻力就可以寫成(其實就是串並聯的電阻而已 ):
再來我們來想像一下,第k級的血管的灌流區域的體積大約是多少呢?我們可以大概想像每個血管的灌流區域大概是一個以血管長度為直徑畫出來的球體,而總灌流區域就是這Nk個分支畫出來的球體的總和。也就是說所有第k級血管總灌流體積為:
到目前為止我們已經大致推導出一些需要的東西,下一集我們就會利用Lagrange
multiplier證明這個系統除了管路數目以外的其他性質也必須遵從碎形,並看看這可以幫助我們推導出甚麼性質。
Comments
Post a Comment