- Get link
- X
- Other Apps
Featured Post
- Get link
- X
- Other Apps
/*--------------Divider --------------*/
The reference of this series is:
本系列文章主要參考資料為:
Drexler, W. & Fujimoto, J. G. (2008). Optical Coherence Tomography - Technology and Applications. 1st ed. NY: Springer.
We will focus on the basic principles of OCT and demonstrate its feasibility by computer simulation. We will not talk about the technical details including the resolution problem, the interaction between tissues and light, and the effect of scattering. We hope everyone could have some inspiration from the design of OCT.
我們會聚焦在OCT的原理,並用程式模擬和大家演示這個東西的可行性。太實務上的議題如解析度、光與組織的交互作用和散射等等不在我們的討論範圍,因為我們的目的是希望讀者能從他一開始的設計得到一些啟發。
/*--------------Divider --------------*/
在開始之前我們當然應該讓大家看看OCT到底是怎樣的一個東西,他是利用干涉解析出來自組織各個層次的反射光的儀器,是optical biopsy的一種。在生醫各個領域都有可能的應用,但目前最well-established的是在眼科視網膜的檢查。病人只要把眼睛湊到機器前面掃一掃,就能得到和組織切片相當的影像品質,著實是一項重大的進步。
Let's see how retina looks like under OCT:
我們來看看用OCT照照視網膜會是長怎樣:
Most of us don't know what a retina should look like, so let's see a standard histology slide:
很多人也許不清楚視網膜應該長怎樣,所以我們附上標準的組織切片圖給大家看一下:
簡單來說就是正常的視網膜應該要有十層結構,而OCT的技術可以讓我們很方便的得到這十層結構的斷面,而不需要把病人的視網膜切一塊下來。
哇嗚不用把病人的視網膜切下來捏~,如果你已經迫不及待想知道他到底是怎麼做到的話,我們就趕快來看看他基本的儀器架設,他其實就是大家很熟悉的麥克生干涉儀,不過和一般的干涉儀不同的是,他使用的光源是一個低度相干的光源,而不是一般常用的高度相干光源,至於為什麼,我們不久之後就會知道。
一道來自光源的光,電場強度為Ei,經過50/50分光鏡後分成兩束光,一道光打在參考反射鏡,另一道光打在樣本上。樣本有許多不同層次,不同層次間因為折射率的不同,在介面處會有反射光。在深度zs的地方反射率為rs(zs)。反射的光又再次回到分光鏡,又各自有一半的光可以打向偵測器,最後我們偵測到的就是來次參考反射鏡與樣本的反射光干涉的結果。(圖片上有個convolution的符號我們先不要理他。)要小提醒的是,因為50/50分光鏡是指把光強分成一半一半,因為光強正比於電場的平方,所以每通過一次分光鏡,電場強度會變成原本的根號2分之一倍喔。而光在打到偵測器之前會經過2次分光鏡,所以電場強度會變成原本的1/2倍。
既然我們已經說明了實驗的基本設置之後,我們就要來給模型中的變數一些設定了(其實就只是對上面的圖裡的算式做一下說明而已)。我們假設當光源第一次抵達分光鏡的時候,電場為Ei,我們可以合理的假設Ei為:
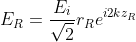
&space;=&space;\sum_{n}&space;r_{S_n}\delta(z_S-z_{S_n}))
The reference of this series is:
本系列文章主要參考資料為:
Drexler, W. & Fujimoto, J. G. (2008). Optical Coherence Tomography - Technology and Applications. 1st ed. NY: Springer.
We will focus on the basic principles of OCT and demonstrate its feasibility by computer simulation. We will not talk about the technical details including the resolution problem, the interaction between tissues and light, and the effect of scattering. We hope everyone could have some inspiration from the design of OCT.
我們會聚焦在OCT的原理,並用程式模擬和大家演示這個東西的可行性。太實務上的議題如解析度、光與組織的交互作用和散射等等不在我們的討論範圍,因為我們的目的是希望讀者能從他一開始的設計得到一些啟發。
/*--------------Divider --------------*/
What OCT could do? 先看看OCT可以幹嘛吧
Before our start we shall see what OCT could do. It could resolve the reflected lights from different histological layers and is also one of the optical biopsy. The most well-established application of OCT is the examination of retina in ophthalmology.在開始之前我們當然應該讓大家看看OCT到底是怎樣的一個東西,他是利用干涉解析出來自組織各個層次的反射光的儀器,是optical biopsy的一種。在生醫各個領域都有可能的應用,但目前最well-established的是在眼科視網膜的檢查。病人只要把眼睛湊到機器前面掃一掃,就能得到和組織切片相當的影像品質,著實是一項重大的進步。
Let's see how retina looks like under OCT:
我們來看看用OCT照照視網膜會是長怎樣:
Figure source:Englander, Miriam; Xu, David; Kaiser, Peter K. (2014). Ophthalmology.1st ed. Fig. 130-2.
Most of us don't know what a retina should look like, so let's see a standard histology slide:
很多人也許不清楚視網膜應該長怎樣,所以我們附上標準的組織切片圖給大家看一下:
Figure source: Ross, M. H., Pawlina, W. (2011). Histology - a Text and Atlas. 6th ed. Fig.24-10.
There are 10 layers in retina, and we could examine the section by OCT without cutting a small piece of the retina of patients. 簡單來說就是正常的視網膜應該要有十層結構,而OCT的技術可以讓我們很方便的得到這十層結構的斷面,而不需要把病人的視網膜切一塊下來。
The setting of OCT OCT的基本儀器架設
Let's first see the experimental setting of OCT. It is actually the Michelson interferometer familiar to most of us. However, the light source is "low-coherent" instead of high-coherent. And we will know why soon.哇嗚不用把病人的視網膜切下來捏~,如果你已經迫不及待想知道他到底是怎麼做到的話,我們就趕快來看看他基本的儀器架設,他其實就是大家很熟悉的麥克生干涉儀,不過和一般的干涉儀不同的是,他使用的光源是一個低度相干的光源,而不是一般常用的高度相干光源,至於為什麼,我們不久之後就會知道。
Figure source:Drexler, W. & Fujimoto, J. G. (2008). Optical Coherence Tomography - Technology and Applications. 1st ed. Fig. 2-3.
The light from light source with electric field Ei is separated into 2 light by a 50/50 beam splitter. One in the reference light path while the other hit upon our sample. There are many layers in our sample, and light reflect between different layers due to the difference in refractive index. Assume the reflectivity at depth zs to be rs(zs). The reflected lights hit the beam splitter again and we only detect the ones hit our detector. We should noted that the light pass through the beam splitter twice and the magnitude of electric field is therefore half the original.一道來自光源的光,電場強度為Ei,經過50/50分光鏡後分成兩束光,一道光打在參考反射鏡,另一道光打在樣本上。樣本有許多不同層次,不同層次間因為折射率的不同,在介面處會有反射光。在深度zs的地方反射率為rs(zs)。反射的光又再次回到分光鏡,又各自有一半的光可以打向偵測器,最後我們偵測到的就是來次參考反射鏡與樣本的反射光干涉的結果。(圖片上有個convolution的符號我們先不要理他。)要小提醒的是,因為50/50分光鏡是指把光強分成一半一半,因為光強正比於電場的平方,所以每通過一次分光鏡,電場強度會變成原本的根號2分之一倍喔。而光在打到偵測器之前會經過2次分光鏡,所以電場強度會變成原本的1/2倍。
The basic setting of our model 模型的基本設定
After some brief explanation about the experimental setting, we could now define some variables for our further analysis. As the light first arrive at the beam splitter, its electric field Ei could be assumed as:既然我們已經說明了實驗的基本設置之後,我們就要來給模型中的變數一些設定了(其實就只是對上面的圖裡的算式做一下說明而已)。我們假設當光源第一次抵達分光鏡的時候,電場為Ei,我們可以合理的假設Ei為:
s(k) represent the spectrum of light source. As the light return back to the beam splitter, assume the length of reference light path z_R and the reflectivity of reference light path r_R, the electric field of light goes reference light path becomes:
s(k)表示光源的光譜分布,我們後面會再看看他的影響。 當兩道光束被分開又再回到分光鏡時,假設參考光徑單趟路程z_R,路上的反射鏡反射率為r_R,則走參考光徑的光現在變成了E_R,我們知道E_R應該可以寫成:
s(k)表示光源的光譜分布,我們後面會再看看他的影響。 當兩道光束被分開又再回到分光鏡時,假設參考光徑單趟路程z_R,路上的反射鏡反射率為r_R,則走參考光徑的光現在變成了E_R,我們知道E_R應該可以寫成:
What about the sample light path? Because our sample have different reflectivity at different depth, its functionality could be written as r_s(z_s). For simplification, it is assumed to be the sum of many delta functions:
我們再來看看sample的地方,因為sample在不同深度有不同的反射率,我們可以假設sample的反射率分布情形為r_s(z_s)。為了方便起見,我們假設他為Dirac delta function的組合,即:
我們再來看看sample的地方,因為sample在不同深度有不同的反射率,我們可以假設sample的反射率分布情形為r_s(z_s)。為了方便起見,我們假設他為Dirac delta function的組合,即:
Because the differences in refractive index across layers are usually small, r_sn << 1, the reflected light could therefore be approximated as:
因為標本各層次之間的折射率落差通常不會很大,所以r_sn通常是個很小的數字,因此反射回來的光可以大約寫成:
因為標本各層次之間的折射率落差通常不會很大,所以r_sn通常是個很小的數字,因此反射回來的光可以大約寫成:
So the current of detector could then be written as:
因此我們最後偵測到的電流則可以寫成:
因此我們最後偵測到的電流則可以寫成:
In which rho means the responsibility of detector. If we set  ,
, 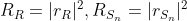 , then the above equation could be expanded as:
, then the above equation could be expanded as:
rho是儀器的反應情形。如果我們令=\left&space;\langle&space;|s(k)|^2&space;\right&space;\rangle) ,
, 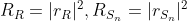 ,則上式可以展開成下面的樣子:
,則上式可以展開成下面的樣子:
rho是儀器的反應情形。如果我們令
There are 3 terms in the detector current. What do they mean? How could they help us delineate the histological layers of our sample? Stay tuned and we will talk about it later.
我們可以看到他有三個項,它們分別代表甚麼呢?它們又要如何幫助我們解出組織的分層情形呢?我們下集再來分曉。
我們可以看到他有三個項,它們分別代表甚麼呢?它們又要如何幫助我們解出組織的分層情形呢?我們下集再來分曉。
- Get link
- X
- Other Apps



Comments
Post a Comment