- Get link
- X
- Other Apps
Featured Post
- Get link
- X
- Other Apps
/*----------Divider----------*/
It's imperative for creatures to sense the gradient of nutrients and poisonous stuffs. The suggested reading we are going to talk about in recent episodes is about how Dictyostelium discoideum, a slime mold, sense the gradient of nutrients. For completeness, we will first discuss the chemotaxis of E. coli in this episode, which most of you may have learned it in your high school or freshman biology courses.
正確察覺環境中養分與有害物質的梯度對於生物的生存非常重要,這次系列的推薦文章是在建立一個針對某種黏菌(Dictyostelium discoideum)如何感應環境中養分梯度的模型。在高中生物或普通生物學的時候應該很多人學過大腸桿菌感應環境養分梯度的模型,為了讓讀者能有比較參照的空間,我們這集會用程式模擬大腸桿菌感應養分梯度的情形,之後兩集再來討論黏菌的情形。
/*----------Divider----------*/
Let's recall how E. coli senses the concentration gradient. E. coli possess 2 motility modes: the "run" mode and the "tumbling" mode. The bacteria run fast and near linearly during the "run" mode while simply changing their direction during the "tumbling" mode. The frequency of tumbling depends on the background concentration of the nutrients. It tumbles less if the concentration of nutrients is high.
我們先簡單回顧一下大腸桿菌是如何感應環境中的梯度。大腸桿菌的運動模式有兩種:衝刺(run) & 翻滾(tumbling),在衝刺模式中大腸桿菌會朝固定方向直線前進,而在翻滾模式中大腸桿菌會原地打轉,讓他可以改變下次衝刺的前進方向。 環境中養分越低,大腸桿菌就越常處於翻滾模式,而環境中養分越高,大腸桿菌就越常處於衝刺模式。就如下圖所示:
The genetic circuit underlying the chemotaxis of bacteria is an interesting topics, but it is not we are going to talk about today. We are always told that using such mechanism, bacteria could successfully migrate toward places with more nutrients. However, no one has ever really demonstrated its success to me. So today we are going to write a simple code to simulate the chemotaxis of bacteria, and check whether such mechanism works.
大腸桿菌感應環境梯度的基因迴路還有很多有趣的東西可以探討,但這不是我們今天的重點。我們今天的重點是要用程式模擬和大家演示說這樣的機制到底有沒有效?以及在甚麼前提條件之下有效?
We write the following codes in MATLAB:
所以我們就寫了下面這樣的程式碼(in MATLAB):
In the codes above, we created a background gradient looks like this. The brighter the site, the more nutrients there are.
在上面的程式碼中,我們造了一個長得像這樣子的環境梯度:(越亮的地方養分越多)
And we have 50 bacteria on it. Their probability of tumbling would increase if they find that there are less nutrients in its surroundings. They compare the concentration of nutrients every τ seconds. Meanwhile we display the average chemotactic index, or CI of these 50 bacteria. The chemotactic index is defined as
然後我們放上了50隻大腸桿菌,如果他們發現環境中的養分越來越少的話,就會傾向改變方向。改變方向的機率和細菌在經過時間τ之後,感應到環境中的養分濃度的「變化」有關。同時我們display出這50隻大腸桿菌平均的CI值(CI = chemotactic index),它的定義是這樣:
The θi is the angle between the direction of bacterial velocity and the direction of actual gradient.
cosine值是由細菌前進的方向和真實的gradient的方向之間的夾角決定的。
Now let's look at their trajectories. Although there are only 8 different colors, the followings actually represents the results from 50 different "artificial" bacteria.
所以我們來看看這50隻大腸桿菌的軌跡會是甚麼樣子:(雖然只有8種顏色,但其實是50隻。)
It looks just "okay" at the first glance. However, the only objective criteria for the performance of chemotaxis is the chemotactic index. So what is the CI for the above result? --- 0.0126. It means that our bacteria waste most of their time tumbling around and did not move along the direction of gradient, even though they eventually move towards the correct side.
看起來其實已經不糟了(當然這也是因為background的梯度被調得有點大),但我們終究是要以可以定量的CI值為依歸。上圖的CI值只有0.0126,表示說細菌大多數的時間並沒有沿著梯度前進,只是花上很長的時間之後會沿著梯度前進而已。
Of course we may try to adjust the above code to make the performance better. If only the bacteria could detect the nutrients in larger area, which should increase the S/N ratio of nutrients detection and gradient sensing. We therefore adjust size_Ecoli from 1 to 3, and the result looks like this:
於是我們當然會想試著調整看看上面的code看能不能變得更好。我們心裡可能會想,把細菌的偵測範圍(程式中的size_Ecoli)調大,會不會比較好。所以我們就把size_Ecoli調整成3,結果長得像這個樣子:
Hmm, it DOES look much better. However, the CI of the above figure is only 0.0309, as terrible as before.
嗯嗯,看起來軌跡似乎是好很多。但我們來看看CI值是多少?───0.0309,一樣的悲劇。
After a little trial and error, it's time to calm down and think carefully about what determines the CI. To answer the question, we drew a schematic diagram like this:
到這裡我們似乎需要冷靜一下,雖然這個系統不算大,但可以被調整的東西其實也是很多的。為了避免盲目嘗試,我們應該想想看到底CI值是由甚麼決定的。所以我們畫出像這樣的模式圖:
Assume that the bacteria is at location r(t) with speed v(t) and speed direction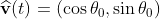 . The number of nutrients it could detect now is ρ(r(t))*A. After time τ, the bacteria now moves to r(t+τ)=r(t)+v*τ*(cosθ0, sinθ0), and the number of nutrients it could detect now is [ρ(r(t))+∇ρ‧vτ]*A. That is to say, the expectation value of the difference in number of detected nutrients after time τ is ∇ρ‧vτA.
. The number of nutrients it could detect now is ρ(r(t))*A. After time τ, the bacteria now moves to r(t+τ)=r(t)+v*τ*(cosθ0, sinθ0), and the number of nutrients it could detect now is [ρ(r(t))+∇ρ‧vτ]*A. That is to say, the expectation value of the difference in number of detected nutrients after time τ is ∇ρ‧vτA.
假設在時間t的時候, 細菌的位置在r(t),速度為v(t),速度方向=(\cos&space;\theta_0,&space;\sin&space;\theta_0)) ,此時他偵測到的養分粒子數為ρ(r(t))*A 。假設細菌每經過時間τ就必須面臨一次是否要改變方向的抉擇,此時他的位置在r(t+τ)=r(t)+v*τ*(cosθ0, sinθ0),而他偵測到的養分粒子數為[ρ(r(t))+∇ρ‧vτ]*A,也就是說兩處偵測到的粒子數變化量的期望值是∇ρ‧vτA。
,此時他偵測到的養分粒子數為ρ(r(t))*A 。假設細菌每經過時間τ就必須面臨一次是否要改變方向的抉擇,此時他的位置在r(t+τ)=r(t)+v*τ*(cosθ0, sinθ0),而他偵測到的養分粒子數為[ρ(r(t))+∇ρ‧vτ]*A,也就是說兩處偵測到的粒子數變化量的期望值是∇ρ‧vτA。
And now let's think about the probability of tumbling. We first assume that it equals p = p(Δn). There are only 2 possibilities:
(1)The bacterium tumbles:
There is a p chance to have cosθi = ∇ρ/|∇ρ|‧(cosθ', sinθ')
(2)The bacterium does not tumble:
There is a (1-p) chance to have cosθi = ∇ρ/|∇ρ|‧v/|v|
It's obvious that the average of ∇ρ/|∇ρ|‧(cosθ', sinθ') = 0 since (cosθ', sinθ') is randomly determined. So to have larger CI, it's necessary to keep the background probability of tumbling a small enough value. That is to say, instead of having a p=p(Δn) which has a functionality looks like the left one, it would be much more preferable if p=p(Δn) has a functionality looks like the right one:
再來我們來想想看關於進入tumbling的機率的部分要怎麼辦。不知道該怎麼辦就先假設他為p,且p = p(Δn)。很顯然就只有兩種結果:
(1)有轉彎:機率p→cosθi = ∇ρ/|∇ρ|‧(cosθ', sinθ')
(2)沒有轉彎:機率1-p→ cosθi = ∇ρ/|∇ρ|‧v/|v|
很顯然的,in the long run,∇ρ/|∇ρ|‧(cosθ', sinθ')的平均值會是0。也就是說,大腸桿菌background的轉彎機率最好不要太大。如果養分濃度是在增加中的,那最好更不要轉彎。但如果養分濃度在減少中,那最好就立刻轉彎。也就是說,p=p(Δn)的函數圖形最好長得像下圖右,而不是像下圖左。
Besides, because the coverage range by a bacterium is quite small. Even though there is no background gradient, the number of nutrients detected in such small area would follows binomial distribution (or Poisson distribution if the nutrients is scarce enough). It would be beneficial to move farther away from the previous site before it to decide whether to tumble or not, since the difference in detected nutrients would be more likely to come from concentration gradient rather than the background noise.
此外,因為能偵測到養分的範圍畢竟是非常小的,裡面的養分粒子數目其實是一個binomial distribution或Poisson distribution(取決於偵測範圍到底有多小,還有養分濃度有多高)。所以移動速度最好快一點,這樣相隔兩次偵測的距離比較遠,偵測的兩處濃度差異越大,偵測梯度的結果越不會受到隨機因素的干擾。
So we adjust our codes as follow:
所以我們把上面的程式碼修改成下面這樣子:
The performance become much better since the CI become 0.3435. In the real world, the distance between tumbling of E. coli is approximately 10 times of its body length. [1] Besides, it is possible to accomplish chemotaxis by adjusting the probability of tumbling with respect to the amount of detected nutrients or repellents. However, it is not the mechanism utilized by slime mold. Would you like to figure it out? Stay tuned and we'll see you next time!
chemotaxis的情況看起來是差不多,但CI值就跳到0.3435囉!而在真實的情況中,大腸桿菌轉彎與轉彎之間間隔的距離,大約是他體長的10倍[1],而藉由改變轉彎機率的方式,也的確能達成chemotaxis的效果。不過在下一集我們要介紹的黏菌,可就不是透過這樣的機制了喔!我們下次再來看看吧~~!
/*----------Divider----------*/
Suggested Readings:
Endres, R. G. & Wingreen, N. S. (2008). Accuracy of direct gradient sensing by single cells. PNAS 105(41): 15749-15754.
Reference:
[1]Patteson, A. E., Gopinath, A., Goulian, M., Arratia, P. E. (2015). Running and tumbling with E. coli in polymeric solutions. Scientific Reports 5: 15761.
It's imperative for creatures to sense the gradient of nutrients and poisonous stuffs. The suggested reading we are going to talk about in recent episodes is about how Dictyostelium discoideum, a slime mold, sense the gradient of nutrients. For completeness, we will first discuss the chemotaxis of E. coli in this episode, which most of you may have learned it in your high school or freshman biology courses.
正確察覺環境中養分與有害物質的梯度對於生物的生存非常重要,這次系列的推薦文章是在建立一個針對某種黏菌(Dictyostelium discoideum)如何感應環境中養分梯度的模型。在高中生物或普通生物學的時候應該很多人學過大腸桿菌感應環境養分梯度的模型,為了讓讀者能有比較參照的空間,我們這集會用程式模擬大腸桿菌感應養分梯度的情形,之後兩集再來討論黏菌的情形。
/*----------Divider----------*/
Let's recall how E. coli senses the concentration gradient. E. coli possess 2 motility modes: the "run" mode and the "tumbling" mode. The bacteria run fast and near linearly during the "run" mode while simply changing their direction during the "tumbling" mode. The frequency of tumbling depends on the background concentration of the nutrients. It tumbles less if the concentration of nutrients is high.
我們先簡單回顧一下大腸桿菌是如何感應環境中的梯度。大腸桿菌的運動模式有兩種:衝刺(run) & 翻滾(tumbling),在衝刺模式中大腸桿菌會朝固定方向直線前進,而在翻滾模式中大腸桿菌會原地打轉,讓他可以改變下次衝刺的前進方向。 環境中養分越低,大腸桿菌就越常處於翻滾模式,而環境中養分越高,大腸桿菌就越常處於衝刺模式。就如下圖所示:
The figure came from the blog of Scientific American. Link:http://blogs.scientificamerican.com/oscillator/files/2011/10/chemotaxis.jpg
The genetic circuit underlying the chemotaxis of bacteria is an interesting topics, but it is not we are going to talk about today. We are always told that using such mechanism, bacteria could successfully migrate toward places with more nutrients. However, no one has ever really demonstrated its success to me. So today we are going to write a simple code to simulate the chemotaxis of bacteria, and check whether such mechanism works.
大腸桿菌感應環境梯度的基因迴路還有很多有趣的東西可以探討,但這不是我們今天的重點。我們今天的重點是要用程式模擬和大家演示說這樣的機制到底有沒有效?以及在甚麼前提條件之下有效?
We write the following codes in MATLAB:
所以我們就寫了下面這樣的程式碼(in MATLAB):
size = 3000;
base = rand(size,size);
grad =
(kron(ones(1,size),(1:1:size)')-size/2)/(0.67*size);
area = round(base + grad +
grad');
t_obs = 200000; dir_all =
{[1,1], [1, 0], [1, -1], [0, 1], [0, -1], [-1, 1], [-1, 0], [-1,-1]};
v = 5; size_Ecoli = 1;
nEcoli = 50;
Ecoli_cell = cell(nEcoli,1);
Ecoli_dir = cell(nEcoli, 1);
for n =
1:nEcoli
xy_series = zeros(t_obs,2); x0 = size/2; y0
= size/2; xy_series(1,:)=[x0, y0]; t_series = zeros(t_obs,1);
dir_series = zeros(t_obs,2); dir =
dir_all{randi(8)}; dir_series(1,:) =
dir;
for t = 1:1:t_obs
if xy_series(t,1) <
(size-size_Ecoli) && xy_series(t,2) < (size-size_Ecoli) &&
xy_series(t,1) > size_Ecoli && xy_series(t,2) > size_Ecoli
t_series(t) =
sum(sum(area(xy_series(t,1)-size_Ecoli:xy_series(t,1)+size_Ecoli,
xy_series(t,2)-size_Ecoli:xy_series(t,2)+size_Ecoli)));
if t>1
del_sum = t_series(t) -
t_series(t-1);
dir_change = round(rand(1,1) -
del_sum/(2*size_Ecoli));
if dir_change
>=1
dir = dir_all{randi(8)};
end
end
xy_series(t+1,:) = xy_series(t,:) +
v*dir;
dir_series(t,:) = dir;
end
end
Ecoli_cell{n} = xy_series;
Ecoli_dir{n} = dir_series;
end
dir_total = zeros(1,nEcoli);
figure, imshow(area); hold on;
for n =
1:nEcoli
xy_series = Ecoli_cell{n};
dir_series = Ecoli_dir{n};
Max = round(nnz(xy_series)/2);
sum_dir = sum(dir_series(:))/(sqrt(2)*Max);
dir_total(n) = sum_dir;
xy_series = Ecoli_cell{n};
plot(xy_series(1:Max,1),
xy_series(1:Max,2), 'LineWidth', 2);
end
display(mean(dir_total));
In the codes above, we created a background gradient looks like this. The brighter the site, the more nutrients there are.
在上面的程式碼中,我們造了一個長得像這樣子的環境梯度:(越亮的地方養分越多)
And we have 50 bacteria on it. Their probability of tumbling would increase if they find that there are less nutrients in its surroundings. They compare the concentration of nutrients every τ seconds. Meanwhile we display the average chemotactic index, or CI of these 50 bacteria. The chemotactic index is defined as
然後我們放上了50隻大腸桿菌,如果他們發現環境中的養分越來越少的話,就會傾向改變方向。改變方向的機率和細菌在經過時間τ之後,感應到環境中的養分濃度的「變化」有關。同時我們display出這50隻大腸桿菌平均的CI值(CI = chemotactic index),它的定義是這樣:
The θi is the angle between the direction of bacterial velocity and the direction of actual gradient.
cosine值是由細菌前進的方向和真實的gradient的方向之間的夾角決定的。
Now let's look at their trajectories. Although there are only 8 different colors, the followings actually represents the results from 50 different "artificial" bacteria.
所以我們來看看這50隻大腸桿菌的軌跡會是甚麼樣子:(雖然只有8種顏色,但其實是50隻。)
It looks just "okay" at the first glance. However, the only objective criteria for the performance of chemotaxis is the chemotactic index. So what is the CI for the above result? --- 0.0126. It means that our bacteria waste most of their time tumbling around and did not move along the direction of gradient, even though they eventually move towards the correct side.
看起來其實已經不糟了(當然這也是因為background的梯度被調得有點大),但我們終究是要以可以定量的CI值為依歸。上圖的CI值只有0.0126,表示說細菌大多數的時間並沒有沿著梯度前進,只是花上很長的時間之後會沿著梯度前進而已。
Of course we may try to adjust the above code to make the performance better. If only the bacteria could detect the nutrients in larger area, which should increase the S/N ratio of nutrients detection and gradient sensing. We therefore adjust size_Ecoli from 1 to 3, and the result looks like this:
於是我們當然會想試著調整看看上面的code看能不能變得更好。我們心裡可能會想,把細菌的偵測範圍(程式中的size_Ecoli)調大,會不會比較好。所以我們就把size_Ecoli調整成3,結果長得像這個樣子:
Hmm, it DOES look much better. However, the CI of the above figure is only 0.0309, as terrible as before.
嗯嗯,看起來軌跡似乎是好很多。但我們來看看CI值是多少?───0.0309,一樣的悲劇。
After a little trial and error, it's time to calm down and think carefully about what determines the CI. To answer the question, we drew a schematic diagram like this:
到這裡我們似乎需要冷靜一下,雖然這個系統不算大,但可以被調整的東西其實也是很多的。為了避免盲目嘗試,我們應該想想看到底CI值是由甚麼決定的。所以我們畫出像這樣的模式圖:
Assume that the bacteria is at location r(t) with speed v(t) and speed direction
假設在時間t的時候, 細菌的位置在r(t),速度為v(t),速度方向
And now let's think about the probability of tumbling. We first assume that it equals p = p(Δn). There are only 2 possibilities:
(1)The bacterium tumbles:
There is a p chance to have cosθi = ∇ρ/|∇ρ|‧(cosθ', sinθ')
(2)The bacterium does not tumble:
There is a (1-p) chance to have cosθi = ∇ρ/|∇ρ|‧v/|v|
It's obvious that the average of ∇ρ/|∇ρ|‧(cosθ', sinθ') = 0 since (cosθ', sinθ') is randomly determined. So to have larger CI, it's necessary to keep the background probability of tumbling a small enough value. That is to say, instead of having a p=p(Δn) which has a functionality looks like the left one, it would be much more preferable if p=p(Δn) has a functionality looks like the right one:
再來我們來想想看關於進入tumbling的機率的部分要怎麼辦。不知道該怎麼辦就先假設他為p,且p = p(Δn)。很顯然就只有兩種結果:
(1)有轉彎:機率p→cosθi = ∇ρ/|∇ρ|‧(cosθ', sinθ')
(2)沒有轉彎:機率1-p→ cosθi = ∇ρ/|∇ρ|‧v/|v|
很顯然的,in the long run,∇ρ/|∇ρ|‧(cosθ', sinθ')的平均值會是0。也就是說,大腸桿菌background的轉彎機率最好不要太大。如果養分濃度是在增加中的,那最好更不要轉彎。但如果養分濃度在減少中,那最好就立刻轉彎。也就是說,p=p(Δn)的函數圖形最好長得像下圖右,而不是像下圖左。
Besides, because the coverage range by a bacterium is quite small. Even though there is no background gradient, the number of nutrients detected in such small area would follows binomial distribution (or Poisson distribution if the nutrients is scarce enough). It would be beneficial to move farther away from the previous site before it to decide whether to tumble or not, since the difference in detected nutrients would be more likely to come from concentration gradient rather than the background noise.
此外,因為能偵測到養分的範圍畢竟是非常小的,裡面的養分粒子數目其實是一個binomial distribution或Poisson distribution(取決於偵測範圍到底有多小,還有養分濃度有多高)。所以移動速度最好快一點,這樣相隔兩次偵測的距離比較遠,偵測的兩處濃度差異越大,偵測梯度的結果越不會受到隨機因素的干擾。
So we adjust our codes as follow:
所以我們把上面的程式碼修改成下面這樣子:
size = 3000;
base = rand(size,size);
grad =
(kron(ones(1,size),(1:1:size)')-size/2)/(1*size);
area = round(base + grad +
grad');
t_obs = 100000; dir_all =
{[1,1], [1, 0], [1, -1], [0, 1], [0, -1], [-1, 1], [-1, 0], [-1,-1]};
v = 80; size_Ecoli = 3;
nEcoli = 50;
Ecoli_cell = cell(nEcoli,1);
Ecoli_dir = cell(nEcoli, 1);
for n =
1:nEcoli
xy_series = zeros(t_obs,2); x0 = size/2; y0
= size/2; xy_series(1,:)=[x0, y0]; t_series = zeros(t_obs,1);
dir_series = zeros(t_obs,2); dir =
dir_all{randi(8)}; dir_series(1,:) =
dir;
for t = 1:1:t_obs
if xy_series(t,1) <
(size-size_Ecoli) && xy_series(t,2) < (size-size_Ecoli) &&
xy_series(t,1) > size_Ecoli && xy_series(t,2) > size_Ecoli
t_series(t) =
sum(sum(area(xy_series(t,1)-size_Ecoli:xy_series(t,1)+size_Ecoli,
xy_series(t,2)-size_Ecoli:xy_series(t,2)+size_Ecoli)));
if t>1
del_sum = t_series(t) -
t_series(t-1);
dir_change = round(rand(1,1) -
0.49 - 80*del_sum/(2*size_Ecoli+1)^2);
if dir_change
>=1
dir = dir_all{randi(8)};
end
end
xy_series(t+1,:) = xy_series(t,:) +
v*dir;
dir_series(t,:) = dir;
end
end
Ecoli_cell{n} = xy_series;
Ecoli_dir{n} = dir_series;
end
dir_total_v5s1 =
zeros(1,nEcoli);
figure, imshow(area); hold on;
for n =
1:nEcoli
xy_series = Ecoli_cell{n};
dir_series = Ecoli_dir{n};
Max = round(nnz(xy_series)/2);
sum_dir = sum(dir_series(:))/(sqrt(2)*Max);
dir_total_v5s1(n) = sum_dir;
xy_series = Ecoli_cell{n};
plot(xy_series(1:Max,1),
xy_series(1:Max,2), 'LineWidth', 2);
end
display(mean(dir_total_v5s1));
And it looks like this:跑跑看結果囉~:The performance become much better since the CI become 0.3435. In the real world, the distance between tumbling of E. coli is approximately 10 times of its body length. [1] Besides, it is possible to accomplish chemotaxis by adjusting the probability of tumbling with respect to the amount of detected nutrients or repellents. However, it is not the mechanism utilized by slime mold. Would you like to figure it out? Stay tuned and we'll see you next time!
chemotaxis的情況看起來是差不多,但CI值就跳到0.3435囉!而在真實的情況中,大腸桿菌轉彎與轉彎之間間隔的距離,大約是他體長的10倍[1],而藉由改變轉彎機率的方式,也的確能達成chemotaxis的效果。不過在下一集我們要介紹的黏菌,可就不是透過這樣的機制了喔!我們下次再來看看吧~~!
/*----------Divider----------*/
Suggested Readings:
Endres, R. G. & Wingreen, N. S. (2008). Accuracy of direct gradient sensing by single cells. PNAS 105(41): 15749-15754.
Reference:
[1]Patteson, A. E., Gopinath, A., Goulian, M., Arratia, P. E. (2015). Running and tumbling with E. coli in polymeric solutions. Scientific Reports 5: 15761.
- Get link
- X
- Other Apps







Comments
Post a Comment