- Get link
- X
- Other Apps
Featured Post
- Get link
- X
- Other Apps
/*-------------Divider-------------*/
There are nectar-feeding species in bees, butterflies, moths, ants, hummingbirds, honeyeaters, sunbirds, and bats. The more concentrated the nectar is, the more energy per unit volume it contains. However, the nectar would also become more viscous and therefore compromise the maximum flow rate. Does this phenomenon place any limitation on nectar-feeding species? How would animals utilizing different nectar-feeding mechanisms be affected differently? That’s what we are going to discuss in these serial episodes and also the research problem that Kim, Gilet and Bush were interested in.
There are nectar-feeding species in bees, butterflies, moths, ants, hummingbirds, honeyeaters, sunbirds, and bats. The more concentrated the nectar is, the more energy per unit volume it contains. However, the nectar would also become more viscous and therefore compromise the maximum flow rate. Does this phenomenon place any limitation on nectar-feeding species? How would animals utilizing different nectar-feeding mechanisms be affected differently? That’s what we are going to discuss in these serial episodes and also the research problem that Kim, Gilet and Bush were interested in.
/*-------------Divider-------------*/
The authors of the suggested
reading consider 3 different nectar-feeding mechanisms. They are
(1)
Active suction utilized by butterflies, moths, and some bees and
ants. These animals produce negative pressure in their oral cavity to suck in
the nectar.
(2)
Capillary suction employed by hummingbirds, honeyeaters, and
sunbirds. These birds intake nectar by capillary flow in the hollow tube formed
by their tongue.
(3)
Viscous dipping exploited by bats, some bees and ants. They
place their tongue into the nectar and rapidly retract it back to their mouth.
In these series, we will talk
about active suction in episode I, capillary suction in episode II, viscous
dipping in episode III, and have extra explanation about LLD theory in episode
IV.
/*-------------Divider-------------*/
Let’s consider the physics
mechanism of active suction. Assume the mouthpiece of butterfly a hollow tube
with inner radius a, tube length L. Assume nectar density ρ, viscosity μ. Assume mean flow velocity in the tube u. Assume the negative pressure produced by butterflies ΔP. According to the Newton’s second
law, we could write down the following for the nectar in the tube:
Inertial force = Pressure
difference X area + Gravitational force + Viscous force
or
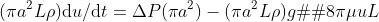
The viscous force might be a
little bit unfamiliar. Please refer to the end of this episode. There are 4
terms in the above equation and it looks terrible, so we are going to remove
some terms by physics reasoning.
How much negative pressure
could be produced by butterflies and moths? Biophysicists believe the work
producible by unit volume of muscles is a constant and therefore the force
producible by muscle is proportional to its cross-section area. (This is
deducible from scaling laws. Please refer to our previous articles: Scaling law of locomotion-I:https://goo.gl/2olyQH
& Scaling law of locomotion-II:https://goo.gl/61l7vv)
Consequently, if it is possible to define a characteristic length L for a creature, the force producible
by it is F ~ L^2. The pressure it
could achieve is therefore
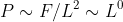
That
is to say all creatures could produce approximately the same negative suction
pressure and that was validate experimentally. The maximum negative pressure
produced by human and mosquitos are both around 10kPa.
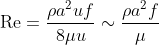
The inner radius of the mouthpiece of butterflies is about 100μm. Substitute the real scale of these variables back and we will get Re ~ 0.1. The inertial force is rather small so we discard it, too.
Finally the equation becomes
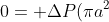&space;-&space;8\pi\mu&space;uL)
That is just Poiseuille flow.
Ultimately we would like to know the relations between the flow rate and viscosity, for they are most easily observed experimentally. A naïve way to deduce the relations would be done by assuming the suction pressure ΔP a constant. Then
u&space;=&space;\Delta&space;P(\pi&space;a^4)/8\mu&space;L&space;\propto&space;\mu^{-1})
Nevertheless, the experimentally observed power law is
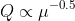
What shall we do? Another possible hypothesis proposed by Pivnick is that the power during active suction is a constant. That is to say
/8\mu&space;L&space;=&space;\textup{Constant})
Because
)
We now arrive at
/(\pi&space;a^4)&space;=&space;\textup{Constant})
So
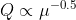
And that is the correct power law observed experimentally.
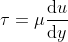
The fluid following this assumption is said to be Newtonian. Those violate this assumption is termed non-Newtonian instead.
That’s then consider a hollow tube streaming Newtonian fluid. Assume the flow is driven by the pressure difference ΔP, the tube length L, inner radius R, fluid density ρ, viscosity μ. Consider the “fluid column” with radial distance less than r. At steady state, the pressure force will balance out the viscous force. We could then write down that:
&space;=&space;\tau&space;(2\pi&space;rL)&space;=\mu&space;\frac{\textup{d}u(r)}{\textup{d}r}(2\pi&space;rL))
or
}{\textup{d}r}=&space;\frac{-\Delta&space;P&space;r}{2&space;\mu&space;L})
Integrate it with the no-slip boundary condition (flow velocity = 0 at r = R) and we will get
&space;=&space;\Delta&space;P(R^2&space;-&space;r^2)/(4\mu&space;L))
The velocity profile is quadratic and it has its maximum value at the central of the tube.
After knowing the velocity profile, it is easy to get the volumetric flow rate Q: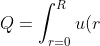(2\pi&space;r)\textup{d}r&space;=&space;\int_{r=0}^{R}\frac{\Delta&space;P(R^2&space;-&space;r^2)}{4\mu&space;L}(2\pi&space;r)\textup{d}r&space;=\frac{\pi\Delta&space;PR^4}{8\mu&space;L})
And this is the well-known Poiseuille’s law for incompressible fluid.
Often we would love to express the flow rate in terms of mean velocity u by assuming
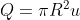
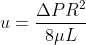
Because the above equation comes from the balance between viscous force and pressure force, the viscous force could be estimated as
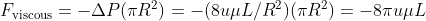
#fluid #mechanics #Poiseuille
What about the gravitational
force? The length of their mouthpiece is about 1cm. Consider the ratio of
gravitational force and pressure force:
It
is small enough compared with the pressure force, so we discard it from our
equation.
So
the Reynold number could now be formulated as
And finally let’s consider
the ratio between the inertial force and viscous force (This is actually the well-known
Reynolds number introduced by Stokes in 1851):
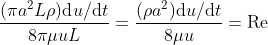
To estimate the term du/dt, assume the suction frequency of butterflies f, which is experimentally observed to be 10 Hz. The acceleration of nectar in the mouthpiece could then be estimated as
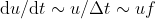
To estimate the term du/dt, assume the suction frequency of butterflies f, which is experimentally observed to be 10 Hz. The acceleration of nectar in the mouthpiece could then be estimated as
The inner radius of the mouthpiece of butterflies is about 100μm. Substitute the real scale of these variables back and we will get Re ~ 0.1. The inertial force is rather small so we discard it, too.
Finally the equation becomes
That is just Poiseuille flow.
Ultimately we would like to know the relations between the flow rate and viscosity, for they are most easily observed experimentally. A naïve way to deduce the relations would be done by assuming the suction pressure ΔP a constant. Then
Nevertheless, the experimentally observed power law is
What shall we do? Another possible hypothesis proposed by Pivnick is that the power during active suction is a constant. That is to say
Because
We now arrive at
So
And that is the correct power law observed experimentally.
/*Supplementary: Poiseuille
flow */
In 17th century,
Newton quantitatively discuss the viscosity of fluid first. He believed that
there would be viscous force whenever there is a velocity gradient between
fluid layers. And the viscous stress τ (the
viscous force per unit area) was “assumed” to be
The fluid following this assumption is said to be Newtonian. Those violate this assumption is termed non-Newtonian instead.
That’s then consider a hollow tube streaming Newtonian fluid. Assume the flow is driven by the pressure difference ΔP, the tube length L, inner radius R, fluid density ρ, viscosity μ. Consider the “fluid column” with radial distance less than r. At steady state, the pressure force will balance out the viscous force. We could then write down that:
or
Integrate it with the no-slip boundary condition (flow velocity = 0 at r = R) and we will get
The velocity profile is quadratic and it has its maximum value at the central of the tube.
After knowing the velocity profile, it is easy to get the volumetric flow rate Q:
And this is the well-known Poiseuille’s law for incompressible fluid.
Often we would love to express the flow rate in terms of mean velocity u by assuming
Substitute it into Poiseuille
law and we will get
Because the above equation comes from the balance between viscous force and pressure force, the viscous force could be estimated as
As what we stated previously.
/*-------------Divider-------------*/
*Suggested reading:
Kim, W., Gilet, T. and Bush, J. W. M. (2011). Optimal
concentrations in nectar feeding. PNAS
108(40): 16618-16621.
#biophysics #3minBiophysics #生物物理 #三分鐘生物物理#fluid #mechanics #Poiseuille
dimensional analysis
fluid mechanics
nectar
ordinary differential equations
Poiseuille flow
Reynolds number
scaling laws
- Get link
- X
- Other Apps


Comments
Post a Comment