- Get link
- X
- Other Apps
Featured Post
- Get link
- X
- Other Apps
The equivalent electrostatics problem等效的靜電學問題
In our previous episode (see: http://biophys3min.blogspot.tw/2016/08/67-gradient-sensing-ii.html) we have derived the particle flow across the surface of a perfectly absorbing sphere without a background gradient. Today, however, we will talk about the expected particle flow across the surface of a perfectly absorbing sphere with a background gradient.在前一集中(http://biophys3min.blogspot.tw/2016/08/67-gradient-sensing-ii.html)我們推導出在沒有背景梯度的情況下,流經perfectly absorbing sphere的粒子流有多大。今天我們要更進一步去討論在有背景梯度的情況下流經perfectly absorbing sphere的粒子流。
Recall our friends, the Fick's law:
再次回顧我們的老朋友Fick's law:
Under steady state, the Fick's second law becomes a Laplace equation.
That shall remind you in electrostatics, the following 2 things:
在穩定狀態下,Fick's second law會變成Laplace equation。上面兩條算式應該會讓你想起在靜電學中我們學過:
在穩定狀態下,Fick's second law會變成Laplace equation。上面兩條算式應該會讓你想起在靜電學中我們學過:
So our original diffusion problem now becomes a standard electrostatics problem:
所以簡單對照一下,我們可以把原本的擴散問題變成一個標準的電磁學課本習題:
所以簡單對照一下,我們可以把原本的擴散問題變成一個標準的電磁學課本習題:
What is the induced surface charge for an uncharged conducting sphere placed in a uniform electric field 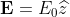 ?
?
當一個導體球放在均勻電場中時,它的表面誘導電荷分布情形為何?
要回答這個問題,我們必須解出球座標中Laplace equation的解。以下的數學會有一點多,但因為這個結果在電磁學、擴散理論和量子力學中都會使用,所以也許稍微介紹一下應該還是ok的。我們要姊的東西長得像這個樣子:
當一個導體球放在均勻電場中時,它的表面誘導電荷分布情形為何?
The solution of Laplace equation in spherical coordinate 球座標中Laplace equation的解
To answer this question, we need the solution of Laplace equation in spherical coordinate. (The following would be a little bit mathematically intensive. However, since it is useful in many fields from electrostatics, diffusion to quantum mechanics, I guess it's still worthwhile to pay some attention to it.) That is the solution of要回答這個問題,我們必須解出球座標中Laplace equation的解。以下的數學會有一點多,但因為這個結果在電磁學、擴散理論和量子力學中都會使用,所以也許稍微介紹一下應該還是ok的。我們要姊的東西長得像這個樣子:
This looks crazy. However, we could break down the monster into pieces by standard technique of separation of variables. By setting=R(r)\Theta(\theta)\Phi(\phi)) . After some manipulation our monster becomes:
. After some manipulation our monster becomes:
他看起來真的很複雜。但是我們可以利用分離變數法把它拆成好幾部分。假設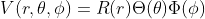 ,帶進去然後利用簡單的加減乘除我們得到:
,帶進去然後利用簡單的加減乘除我們得到:
他看起來真的很複雜。但是我們可以利用分離變數法把它拆成好幾部分。假設
The RHS of equation is a constant while the LHS of equation has 3 terms with different variable-dependency. Therefore we could readily assume:
方程式的右手邊是一個常數,但左手邊的每個項卻是不同變數的函數,所以要能相加等於常數的唯一可能就是這些函數其實各自都是常數。也就是說我們可以假設:
方程式的右手邊是一個常數,但左手邊的每個項卻是不同變數的函數,所以要能相加等於常數的唯一可能就是這些函數其實各自都是常數。也就是說我們可以假設:
And our Φ is obviously
現在 Φ的部分就很簡單囉:
現在 Φ的部分就很簡單囉:
The m must be an integer because we expect the function to satisfy=\Phi(\phi)) .
.
因為我們希望Φ可以滿足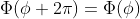 ,所以m必須是整數。
,所以m必須是整數。
The rest part of equation could be manipulated in basically the same way, by:
剩下的部分也可以利用相同的方法把他分離變數之後假設成:
因為我們希望Φ可以滿足
The rest part of equation could be manipulated in basically the same way, by:
剩下的部分也可以利用相同的方法把他分離變數之後假設成:
The l(l+1) might look strange to you. Nevertheless, it will prove its own benefit soon. Let's see the R part first:
右手邊我們假設成l(l+1),看起來很奇怪,可是等一下我們就會看到它的好處了。先看R的部分:
右手邊我們假設成l(l+1),看起來很奇怪,可是等一下我們就會看到它的好處了。先看R的部分:
The 3 terms has the same power of r (the Cauchy-Euler equation), therefore the solution could be assumed to be R = r^s. Substitute it back would be:
注意到方程式的三個項其實是r的相同冪次,這樣的微分方程式我們稱為 Cauchy-Euler equation。這種方程式的解可以假設成R = r^s,把他帶回去就會得到:
注意到方程式的三個項其實是r的相同冪次,這樣的微分方程式我們稱為 Cauchy-Euler equation。這種方程式的解可以假設成R = r^s,把他帶回去就會得到:
The Θ is definitely the "boss" of the game. It now looks like:
Θ顯然在這裏是最難解的大魔王,他的方程式現在長得像這樣:
Θ顯然在這裏是最難解的大魔王,他的方程式現在長得像這樣:
It would be too messy to demonstrate the full process of solving. If you are interested in that, try to assume w = cosθ and assume 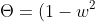^{|m|/2}F(w)) . And it will turns out that the solution is an associated Legendre polynomial which could be also defined by the Rodrigues formula:
. And it will turns out that the solution is an associated Legendre polynomial which could be also defined by the Rodrigues formula:
要解他真的是個大工程,所以我們不把冗長的計算放上來。如果你有興趣,你可以假設
w = cosθ然後再假設 ,用級數解展開然後算一算,最後的答案會是associated Legendre polynomial。他有好幾種表達方式,其中比較好用的是用Rodrigues formula表示:
,用級數解展開然後算一算,最後的答案會是associated Legendre polynomial。他有好幾種表達方式,其中比較好用的是用Rodrigues formula表示:
因為我們討論的問題具有方位角對稱,所以我們直接利用m=0,我們的解就可以表示成:
要解他真的是個大工程,所以我們不把冗長的計算放上來。如果你有興趣,你可以假設
w = cosθ然後再假設
For a system with azimuthal symmetry, m = 0 and the solution could then be expressed as Legendre polynomials.
如果我們探討的系統具有方位角對稱,那m = 0,我們的系統的解就可以表示成Legendre polynomials。
如果我們探討的系統具有方位角對稱,那m = 0,我們的系統的解就可以表示成Legendre polynomials。
The solution expressed by sum of (associated) Legendre polynomials is cool. However, We hope to have some "basis" that is orthonormal (that is both orthogonal and normalized) rather than merely orthogonal. So it is also common to express our solution using spherical harmonics instead:
用 (associated) Legendre polynomials的加總來表示我們的解通常已經蠻夠用。但有時候我們希望我們的解彼此是標準正交而不僅僅是正交(不同的Legendre polynomials是彼此正交的,就和傅立葉分析的時候不同的sin cos是彼此正交的),所以我們可以把Legendre polynomial標準化之後得到球諧函數:
用 (associated) Legendre polynomials的加總來表示我們的解通常已經蠻夠用。但有時候我們希望我們的解彼此是標準正交而不僅僅是正交(不同的Legendre polynomials是彼此正交的,就和傅立葉分析的時候不同的sin cos是彼此正交的),所以我們可以把Legendre polynomial標準化之後得到球諧函數:
Now back to our electrostatics problem...現在回到電磁學問題
Because our problem possesses azimuthal symmetry, the solution could therefore expressed as:因為我們討論的問題具有方位角對稱,所以我們直接利用m=0,我們的解就可以表示成:
It still does not look easy. Let's calm down and think about it. Because there is a background electric field and we know the electric field is basically the gradient of electric potential. So in somewhere far far away, the potential would definitely forget he has encountered a crazy sphere floating somewhere. That means:
hmm他看起來還是有點複雜欸,我們稍微冷靜思考一下。因為我們有一個均勻電場,其實就是均勻的電位梯度。想想看在距離導體球無窮遠的彼方,電場怎麼可能還會記得說他曾經遇到這麼一個小小的導體球呢?也就是說當z→無窮大時,電位可以表示成:
hmm他看起來還是有點複雜欸,我們稍微冷靜思考一下。因為我們有一個均勻電場,其實就是均勻的電位梯度。想想看在距離導體球無窮遠的彼方,電場怎麼可能還會記得說他曾經遇到這麼一個小小的導體球呢?也就是說當z→無窮大時,電位可以表示成:
Since a conducting ball is an equipotential and the system possess symmetry, we could assume the potential of entire x-y plane and the sphere to be 0. So the constant C must be 0, too. And because r cosθ = z, so only the term with l = 1 would survive. Check the table of Legendre polynomial and we will know that =\cos\theta) , so the solution we are craving for now becomes
, so the solution we are craving for now becomes
因為導體球是等電位的,而且我們的系統具有很好的對稱性,我們可以假設整個x-y平面以及球體的電位=0。所以上面的常數C就是0。同時因為 r cosθ = z,所以只有l = 1的項可以存活下來,剩下其他項如果保留的話就無法滿足前面的漸進性質。查表一下我們就知道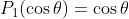 ,所以現在解就可以化簡成:
,所以現在解就可以化簡成:
因為導體球是等電位的,而且我們的系統具有很好的對稱性,我們可以假設整個x-y平面以及球體的電位=0。所以上面的常數C就是0。同時因為 r cosθ = z,所以只有l = 1的項可以存活下來,剩下其他項如果保留的話就無法滿足前面的漸進性質。查表一下我們就知道
It now looks much more friendly, right? Now by knowing that V = 0 when r = R, and V→-Ez, it is easy to show that
看起來真是順眼多了。現在我們利用 V = 0 when r = R, and V→-Ez,我們就可以求得:
看起來真是順眼多了。現在我們利用 V = 0 when r = R, and V→-Ez,我們就可以求得:
chemotaxis
diffusion
electromagnetism
Fick's law
gradient sensing
Legendre polynomials
partial differential equation
spherical harmonics
- Get link
- X
- Other Apps

Comments
Post a Comment