#8 The optimal concentration of nectar-III

/*-------------Divider-------------*/
Please finish reading episode 6 before reading. Today we are going to talk about the physics of viscous dipper. The physics of viscous dipper requires the results of Landau-Levich-Derjaguin Theory, which we will talk about in next episode.

/*------------- Divider -------------*/

Actually, the mechanisms of active sucker and capillary sucker are not proposed by Kim, Gilet and Bush. Instead, they are finished by J. G. Kingsolver, T. L. Daniel, and K. A. Pivnick with more than 30 years. The mechanism we are going to talk about today, the viscous dipper, is the one proposed by the authors.

Before the quantitative discussion, let’s have some qualitative thought experiments. The mechanism of viscous dipper is just like dipping sashimi in soy sauce. Bumblebees(Bombus) and honeybees(Apis) are viscous dipper. (Some bee genus are active sucker.) Now consider a piece of sashimi half dipped in soy sauce. If we take out the sashimi with speed extremely slow, how much soy sauce could be extracted from the sauce dish? Nothing! Because all soy sauce flows back to sauce dish due to gravity. Then what if we take out the sashimi with speed extremely fast? The amount of sauce extracted is still 0 because there is no time for the soy sauce to attach. Therefore, we now understand that the amount of soy sauce extractable by the sashimi strongly depends on the speed we take it out, and the functionality should be nonlinear.

Instinctively, the amount of soy sauce extracted could be calculated by knowing the surface area of sashimi S and the thickness of soy sauce on the surface of sashimi e. It is the thickness e that depends on speed of retraction. After these basic understanding, we will now delve into the quantitative discussion.

/*----Physics Discussion----*/

Assume that the mouthpiece of honeybee dipped into the nectar a column with radius a and length L (assume L>>a). Assume the retraction speed u, thickness of nectar attached e, time required for protrusion or retraction T, intervals between dipping T0. The average volumetric flow rate Q could then be expressed as 

This should be readily understandable. Next we will derive how Q depends on μ using dimensional analysis. Because the “fixed power assumption” proposed by Pivnick in 1985 successfully solved the problem encountered by Kingsolver & Daniel (that Q ∝ μ^(-1/2) rather than Q ∝ μ^(-1)), Kim, Gilet and Bush followed this assumption in the following discussion. What work should be done by honeybees as they retract their tongues from nectar? One is the viscous work Wv required for combating the viscous force. The other is the acceleration work Wt required for mobilizing a resting tongue. The power associated with them is termed Pv and Pt, respectively.

Let’s first consider Pv. The unit of power is N-m/s. We expect the work required to resist the viscous force would be larger if the viscosity μ becomes larger, the length of tongue L becomes longer, or the retraction speed u becomes faster. The units of them are [μ]=Pa-s=N-s/m^2, [L]=m, and [u]=m/s. So by dimensional analysis, it is expected that

Next we consider Pt. Since the power could be expressed as the inner product of force and speed. Given the mass of tongue m, the power could be easily written as

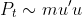
Since the density of tongue and the density of nectar is about the same, the above expression could be approximated by

The acceleration u’ could be estimated by the speed divided by the time of retraction or protrusion. Since the time required is approximately t ~ L/u, so


Substitute it back to Pt and we will get

Now there are 2 powers and their sum should be fixed. However, it is troublesome to consider both terms at once. So we would like to discard one of them. Consider the ratio

According to the high-speed photography, u ~ 2cm/sec, L~2mm, and a~0.1mm. Given the viscosity of water μ~9x10^(-4)Pa-s, the ratio is about 0.1. Since the viscosity of nectar is even larger, Pt is negligible compared to Pv. That is to say, according to the hypothesis of fixed power,

Or


Substitute back to our expression of average volumetric flow rate

 

Since the ratio T/(2T+T0) does not depend on viscosity, we could derive that

In the next episode, we will derive e with LLD theory and finish the discussion about viscous dipper. Stay tuned!

/*------------- Divider -------------*/

Suggested reading:

Kim, W., Gilet, T., and Bush, J. W. M. (2011). Optimal concentrations in nectar feeding. PNAS 108(40): 16618-16621.

‪#‎biophysics ‪#‎3minBiophysics ‪#‎生物物理 ‪#‎三分鐘生物物理
‪#‎scaling law ‪#‎viscosity ‪#‎bee