- Get link
- X
- Other Apps
Featured Post
- Get link
- X
- Other Apps
/*-------------Divider-------------*/
After some discussion about the theory of diffusion, we could then talk about the model proposed by the authors. They proposed that the heat of reaction could locally deform the enzyme and propel themselves by the reaction force given by solvent. Today we are going to estimate the pressure that could be generated by the compression of solvent.
/*-------------Divider------------*/
/*-------------Divider------------*/
The negative sign comes from the fact that pressure increases as volume decreases. The compressibility measured in isothermal process and adiabatic process are actually different. However, such difference is generally negligible for liquid and solid. Assume the pressure from solvent act on somewhere different from the center of enzyme, and its direction is 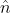 . We can then write down the pressure term:
. We can then write down the pressure term:
Under the assumption of azimuthal symmetry, the net pressure force would only act on z direction. Since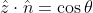 ,
,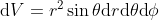 . We then write
. We then write
Integrate the above from φ=0~2π, θ=0~π/2, and we will get
Assume the heat of reaction could increase its radius by ΔR from R, then we could write down:
To estimate its magnitude, given the compressibility of water = 4.475x10^(-10)Pa, the radius of enzyme = 4nm, and the change in radius ~ 1nm, the calculated pressure is about 1064pN/nm^2. It is a large number compared to the thermal pressure kT/V = 0.017pN/nm^2. However, the pressure is overestimated since the generation of sound wave is not accounted in previous discussion. The following would yield a more reasonable estimation.
Now let's consider the situation with sound wave generated. Since the energy released from chemical reaction is what we definitely know, not the magnitude of enzyme deformation, we would like to link the energy and pressure together. Recall that the intensity of sound wave could be written as (Refer to the supplementary below if you don't know why)
After some arithmetics, assume the heat of reaction = 40kT, it could be re-written as
The time t is the time scale required for the spreading of pressure wave in enzyme, which could be estimated from the compressibility, density and radius of enzyme. The final pressure estimated is 51pN/nm^2 and the magnitude of deformation is 0.06nm. This is a much more reasonable and obtainable magnitude.
The time t is the time scale required for the spreading of pressure wave in enzyme, which could be estimated from the compressibility, density and radius of enzyme. The final pressure estimated is 51pN/nm^2 and the magnitude of deformation is 0.06nm. This is a much more reasonable and obtainable magnitude.
/*Supplementary*/
The intensity of sound wave could be derived from impedance. The impedance Z is defined as the ratio between pressure p and the speed of medium molecules v, or
The intensity of sound wave could be derived from impedance. The impedance Z is defined as the ratio between pressure p and the speed of medium molecules v, or
Consider a one dimensional wave, the amplitude of medium is assumed to be trigonometric
From the definition of compressibility
From the definition of compressibility
- Get link
- X
- Other Apps
Comments
Post a Comment