Hello everyone. Happy Chinese New Year! Today I am going to greet our readers with my humble gift, the Brownian Carnot engine model.
If you are not familiar with the Carnot engine, please refer to our older post: https://goo.gl/QySuJE.
/*-----------------Divider-----------------*/
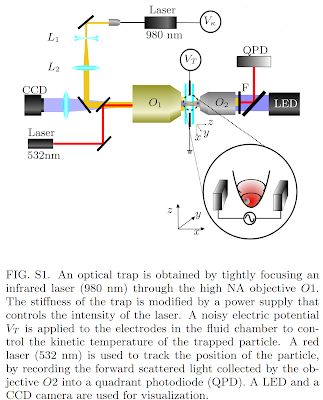
The Carnot cycle proposed in 1824 sets an upper limit to the efficiency of thermal engines. However, does that still hold in the microscopic world, in which most biological motors operate? In order to experimentally study how a microscopic Carnot engine would work, the authors of our suggested reading developed a way that could effectively heat, cool, compress or expand a microsphere confined to the optical tweezers, as shown below.
This also implies that if we push the microsphere to increase its range of motion, we could then effectively heat the system. This is feasible since the polystyrene beads have an inherent charge in polar solutions, and we could adjust its range of motion by applying random voltage.
After introducing this system, we will now reformulate heat, work, and other key variables in our system. First we write down the Hamiltonian of the system:
^2+\frac{p^2}{2m},\quad&space;p=m\frac{\textup{d}x}{\textup{d}t} "H = \frac{1}{2}\kappa x(t)^2+\frac{p^2}{2m},\quad p=m\frac{\textup{d}x}{\textup{d}t}")
The conjugated force associated with the external variable κ could be obtained by
^2 "F_{\kappa}=\frac{\partial H}{\partial \kappa} =\frac{1}{2}x(t)^2")
and the work must be done to change κ would be
=F_{\kappa}(t)\textup{d}\kappa "{\mathchar'26\mkern-12mu \textup{d}}W(t)=F_{\kappa}(t)\textup{d}\kappa")
and the heat could be calculated as
=\textup{d}H-{\mathchar'26\mkern-12mu&space;\textup{d}}W(t) "{\mathchar'26\mkern-12mu \textup{d}}Q(t)=\textup{d}H-{\mathchar'26\mkern-12mu \textup{d}}W(t)")
It's much more easier to figure out how we could perform an isothermal compression or expansion on this system. What about the adiabatic ones? In a microscopic regime, we could obtain a process during which
\right&space;\rangle=\left&space;\langle\textup{d}H\right&space;\rangle-\left&space;\langle{\mathchar'26\mkern-12mu&space;\textup{d}}W(t)\right&space;\rangle=0 "\left \langle {\mathchar'26\mkern-12mu \textup{d}}Q(t)\right \rangle=\left \langle\textup{d}H\right \rangle-\left \langle{\mathchar'26\mkern-12mu \textup{d}}W(t)\right \rangle=0")
and thus implies
which means
hold during an adiabatic process. So now we know how to build and run a Brownian Carnot engine conceptually.
In the next episode, in contrary to what the authors did, we are going to simulate a Brownian Carnot engine (rather than really build one) and plot the experiment results. Stay tuned!
/*-----------------Divider-----------------*/
Suggested reading: Martinez, I. A., Roldan, E., Dinis, L., Petrov, D., Parrondo, J. M. R., Rica, R. A. (2015). Brownian Carnot Engine. Nature Physics 12, 67-70.
Reference
[1]Martínez, I. A., Roldán, E., Dinis, L., Petrov, D. and Rica, R. A. (2015) Adiabatic processes realized with a trapped Brownian particle. Phys. Rev. Lett. 114, 120601.
If you are not familiar with the Carnot engine, please refer to our older post: https://goo.gl/QySuJE.
/*-----------------Divider-----------------*/
The Carnot cycle proposed in 1824 sets an upper limit to the efficiency of thermal engines. However, does that still hold in the microscopic world, in which most biological motors operate? In order to experimentally study how a microscopic Carnot engine would work, the authors of our suggested reading developed a way that could effectively heat, cool, compress or expand a microsphere confined to the optical tweezers, as shown below.
(figure adapted from the supplementary figure 1 of ref[1].)
The optical tweezers could act as an effective spring with force constant κ, which confines the range of motion of the microsphere. Thus, by adjusting the force constant κ, we could effectively compress or expand the volume of the system. Besides, by recording the position of the microsphere, we could deduce the temperature if we know the force constant κ, because:After introducing this system, we will now reformulate heat, work, and other key variables in our system. First we write down the Hamiltonian of the system:
It's much more easier to figure out how we could perform an isothermal compression or expansion on this system. What about the adiabatic ones? In a microscopic regime, we could obtain a process during which
In the next episode, in contrary to what the authors did, we are going to simulate a Brownian Carnot engine (rather than really build one) and plot the experiment results. Stay tuned!
/*-----------------Divider-----------------*/
Suggested reading: Martinez, I. A., Roldan, E., Dinis, L., Petrov, D., Parrondo, J. M. R., Rica, R. A. (2015). Brownian Carnot Engine. Nature Physics 12, 67-70.
Reference
[1]Martínez, I. A., Roldán, E., Dinis, L., Petrov, D. and Rica, R. A. (2015) Adiabatic processes realized with a trapped Brownian particle. Phys. Rev. Lett. 114, 120601.
Comments
Post a Comment