- Get link
- X
- Other Apps
Featured Post
- Get link
- X
- Other Apps
Today we will progress to the theoretical parts.
今天我們要進展到理論解析的部分囉~!
我們先呼叫上集最後面出現的電流,其實三個項的意思非常非常簡單:
The second term contains the effect of interference between the reference optical path and the reflected light from each histological layers. We call it "Cross-correlation terms" because it contains information across different optical path. Since we know R_R&Zsr already, if we could select out these terms we could easily know Rsn & zsn, which is just what we are craving for.
The third term contains the interference between different reflective layers and is called "Auto-correlation terms". This term is troublesome because it contains too much unknown parameters. Fortunately the reflectivity between different layers of sample is "usually" small enough for us to simply neglect this term. (I mean "USUALLY" but not always.)
S(k) is usually assumed to be Gaussian. That is![S(k)=\frac{1}{\Delta k \sqrt{\pi}}e^{-[\frac{(k-k_0)}{\Delta k}]^2}](https://latex.codecogs.com/gif.latex?S%28k%29=%5Cfrac%7B1%7D%7B%5CDelta&space;k&space;%5Csqrt%7B%5Cpi%7D%7De%5E%7B-[%5Cfrac%7B%28k-k_0%29%7D%7B%5CDelta&space;k%7D]%5E2%7D) . Namely, if we have a spectrometer which could detect the intensity of single wavelength and we scanned it for the whole spectrum, the results would look like a Gaussian modulated by many cosine terms. Like this:
. Namely, if we have a spectrometer which could detect the intensity of single wavelength and we scanned it for the whole spectrum, the results would look like a Gaussian modulated by many cosine terms. Like this:
S(k)通常我們會假設成Gaussian,即![S(k)=\frac{1}{\Delta k \sqrt{\pi}}e^{-[\frac{(k-k_0)}{\Delta k}]^2}](https://latex.codecogs.com/gif.latex?S(k)=\frac{1}{\Delta&space;k&space;\sqrt{\pi}}e^{-[\frac{(k-k_0)}{\Delta&space;k}]^2}) 。所以說,如果我們有一個波長選擇器,可以只偵測單一波長的光強度,然後我們對不同波長來掃強度的話,他就會像是一個Gaussian被好多個cosine調節。長得就像這樣子:
。所以說,如果我們有一個波長選擇器,可以只偵測單一波長的光強度,然後我們對不同波長來掃強度的話,他就會像是一個Gaussian被好多個cosine調節。長得就像這樣子:
今天我們要進展到理論解析的部分囉~!
What are the 3 current terms? 電流的三個項是怎麼回事?
Let's recall the current we mentioned in the previous episode:
我們先呼叫上集最後面出現的電流,其實三個項的意思非常非常簡單:
The first term is simply the summation of the intensity of all reflected light without interference. This is just like a direct current and is therefore called "DC term."
第一個項其實蠻簡單的,其實就是每道反射光的光強直接加起來。如果只有這一項的話,表示每道反射光之間完全不相干涉的意思。這個項又被稱為"DC term",因為他就像直流電一樣。
第一個項其實蠻簡單的,其實就是每道反射光的光強直接加起來。如果只有這一項的話,表示每道反射光之間完全不相干涉的意思。這個項又被稱為"DC term",因為他就像直流電一樣。
The second term contains the effect of interference between the reference optical path and the reflected light from each histological layers. We call it "Cross-correlation terms" because it contains information across different optical path. Since we know R_R&Zsr already, if we could select out these terms we could easily know Rsn & zsn, which is just what we are craving for.
第二項當然就是干涉的項囉,他就是參考光徑的反射光與組織每層的反射光彼此干涉的項,研究者稱之為"Cross-correlation terms",因為他是參考光徑與樣本光徑的光之間的關係。因為我們想知道的東西是Rsn & zsn,而R_R&Zsr都是我們已知的東西,很容易除掉,所以這個項是我們最想要保存的東西。
The third term contains the interference between different reflective layers and is called "Auto-correlation terms". This term is troublesome because it contains too much unknown parameters. Fortunately the reflectivity between different layers of sample is "usually" small enough for us to simply neglect this term. (I mean "USUALLY" but not always.)
那第三項各位一定能依此類推了,他就是組織不同層的反射光之間彼此干涉的項,研究者稱之為"Auto-correlation terms",因為他是樣本光徑之內不同道光之間的關係。這個項會給我們帶來一些麻煩,但幸好樣本各層次的反射率並不大,遠遠小於參考光徑的反射率,所以通常這個項會很小(我說是「通常」喔)。
It is obvious that the exp(i~) + exp(-i~) could be written in terms of cosine. So let's do that:
眼尖的各位一定可以看出來,exp(i~)+ exp(-i~)根本就可以寫成cosine嘛。的確是這樣沒錯,所以我們就把它寫下來:
S(k) is usually assumed to be Gaussian. That is
S(k)通常我們會假設成Gaussian,即
The period of each modulation cosine equals 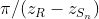 , and different terms have different period. We are going to delineate some information from this. There are 2 ways: Fourier domain OCT (abbreviated as FDOCT) & Time domain OCT (abbreviated as TDOCT).
, and different terms have different period. We are going to delineate some information from this. There are 2 ways: Fourier domain OCT (abbreviated as FDOCT) & Time domain OCT (abbreviated as TDOCT).
每一個調節的cosine在k-domain的週期 =) ,來自不同項的週期並不相同。我們就是要從這裏面隱藏的資訊解出不同層的反射率。基本上有兩種方法:Fourier domain OCT(以下簡稱為FDOCT)、Time domain OCT(以下簡稱TDOCT)。
,來自不同項的週期並不相同。我們就是要從這裏面隱藏的資訊解出不同層的反射率。基本上有兩種方法:Fourier domain OCT(以下簡稱為FDOCT)、Time domain OCT(以下簡稱TDOCT)。
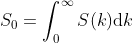 . Recall we said previously S(k) is assumed to be a Gaussian, so its integration = 1. Assume k0>2Δk, the integration reads:
. Recall we said previously S(k) is assumed to be a Gaussian, so its integration = 1. Assume k0>2Δk, the integration reads:
因為這比較簡單所以先講。如果我們在偵測光強時,並沒有放上波長選擇器,那麼我們測到的就是來自所有波長的能量總和,相當於把電流對k做積分。我們假設\textup{d}k) 。還記得我們剛剛才講過我們假設S(k)是Gaussian,積分其實就等於1。我們簡單積分一下下面這個東西(如果k0>2Δk):
。還記得我們剛剛才講過我們假設S(k)是Gaussian,積分其實就等於1。我們簡單積分一下下面這個東西(如果k0>2Δk):
The strange R means "take real part." From above we know:
有個奇怪的R是取實部的意思。從上面我們就知道:
We could understand why we should use a low-coherent light source. A low-coherent light source have broad spectrum (which means large Δk). The above formula shows that we will get sharper peaks if the Δk is large. We will get very broad peaks in our TDOCT scanning results if we use a laser as light source instead.
This is also instinctive. If the light source are low-coherent, only if we adjust the reference optical path length near the distance of certain reflective layer will they be able to interfere with each other. If the light source is highly coherent, the light from reference light path could simultaneously interfere with light reflected from layer 1, layer 2, ... and layer n and therefore becomes troublesome. That's the reason why we should use a low-coherent light source.
TDOCT looks simple enough and performs well. However, there are some difficulty utilizing it in every scenario. First, its resolution is limited by how precisely we could adjust the reference optical path length. We must be able to adjust the reference optical path length by 1 micrometer if we want a 1 micrometer resolution. It is also apparently time-consuming if we have a thick sample.
And that's why we need FDOCT. We will discuss it in next episode. Stay tuned!
每一個調節的cosine在k-domain的週期 =
TDOCT
We will talk about TDOCT first because it is much simpler. If we don't use a spectrometer and measure the intensity directly, we are measuring the sum of all intensity from different wavelengths. This is equivalent to integrate the current with respect to k. Assume that因為這比較簡單所以先講。如果我們在偵測光強時,並沒有放上波長選擇器,那麼我們測到的就是來自所有波長的能量總和,相當於把電流對k做積分。我們假設
The strange R means "take real part." From above we know:
有個奇怪的R是取實部的意思。從上面我們就知道:
Now only the cross-correlation terms preserved its dependency on z_R. That is to say we could consider DC term and autocorrelation terms a constant as we changes the reference optical path length. The results would look like this:
上面的電流只剩下中間的項會隨z_R改變,也就是說只要我們紀錄z_R改變的情況下,所有波長的電流總讀值,就可以自動把DC & autocorrelation的項變成常數,所以畫出來的圖大概會長這樣:
上面的電流只剩下中間的項會隨z_R改變,也就是說只要我們紀錄z_R改變的情況下,所有波長的電流總讀值,就可以自動把DC & autocorrelation的項變成常數,所以畫出來的圖大概會長這樣:
In this figure there are 7 reflective surface in our scanning range.
從這張圖我們可以看出這個sample在我們掃描的這個範圍裡有7個反射介面。
從這張圖我們可以看出這個sample在我們掃描的這個範圍裡有7個反射介面。
We could understand why we should use a low-coherent light source. A low-coherent light source have broad spectrum (which means large Δk). The above formula shows that we will get sharper peaks if the Δk is large. We will get very broad peaks in our TDOCT scanning results if we use a laser as light source instead.
從這裡我們就可以知道為什麼我們應該用低度相干光源。低度相干光源的頻譜分得很散(Δk很大),從上面的算式我們可以看出Δk越大,每個介面造成的Gaussian分布就越窄。如果我們使用雷射來進行OCT,因為雷射為高度相干光源,Δk非常小,那用在這裡每個Gaussian就會變得非常非常寬。
This is also instinctive. If the light source are low-coherent, only if we adjust the reference optical path length near the distance of certain reflective layer will they be able to interfere with each other. If the light source is highly coherent, the light from reference light path could simultaneously interfere with light reflected from layer 1, layer 2, ... and layer n and therefore becomes troublesome. That's the reason why we should use a low-coherent light source.
其實從物理直覺來想也是很清楚的。因為如果光源相干性非常差,那只有當我們把參考光徑的長度調整到大約等於特定某層的反射光徑時,才會出現干涉條紋(因為兩條光路的時間差還在相干時間之內),只要再稍微超出一點點就不會有干涉。如果相干性很好的話,參考光徑的光可以同時和來自第一層、第二層、第...層的光一起干涉,那就變得非常難解析了。這就是為什麼要用低度相干光源的原因。
TDOCT looks simple enough and performs well. However, there are some difficulty utilizing it in every scenario. First, its resolution is limited by how precisely we could adjust the reference optical path length. We must be able to adjust the reference optical path length by 1 micrometer if we want a 1 micrometer resolution. It is also apparently time-consuming if we have a thick sample.
TDOCT看起來很不錯,但他其實還是會有一些困難,首先我們的解析度會受限於我們調整參考光徑的解析度,所以如果我們想要得到1微米的解析度,我們就必須能夠精確調整參考光徑的長度1微米。而且重點是想想看如果我們是要去掃一整片影像的時候,或是這個儀器掃描長度1000次等等,都必須要能維持同樣的精確度。而且如果我們要掃的厚度比較厚,比方說1cm好了,就表示我們要精確調整1微米1微米1微米直到1cm為止,這電腦模擬模擬一下很快,真實世界可是非常耗時的呢!
And that's why we need FDOCT. We will discuss it in next episode. Stay tuned!
那這樣該怎麼辦呢?我們下集會再來探討另一種方法,FDOCT。
- Get link
- X
- Other Apps


Comments
Post a Comment