- Get link
- X
- Other Apps
Featured Post
- Get link
- X
- Other Apps
/*---------Divider---------*/
In the Chinese version, this was the first article in 3min Biophysics. In this episode, we are going to discuss the physics of how cats drink water. The suggested reading (which is also the original journal article) could be found below. And the Chinese version of this episode could be found in 貓喝水的物理:https://goo.gl/SJIZCM.
/*---------Divider---------*/
Most mammals, including human, could suck in water with the negative pressure produced by the contraction of buccinator muscle. However, the mammals which belongs to the Carnivora cannot simply suck in water as we do, since their buccinator muscles have evolved into U-shaped in order to permit wider opening of their mouth. How do cats drink water efficiently?
With the aids of high-speed imaging, Reis and their colleagues could closely observe how cat "laps" water. They found that during the lapping process, the tongues of cats do not penetrate the water surface. Instead, the tip of tongue touches the water surface and rapidly elevates, which brings up a water column. The cat then close its mouth to ingest the water just have been brought up by its tongue.
However, is that really a physically feasible mechanism to drink water? Does this mechanism impose any limitation on cats? That's what a biophysicist care about. Therefore, Reis and their colleagues made an artificial tongue model to analyze the mechanism of lapping water and used dimensional analysis to make prediction about how the lapping frequency varies with animal sizes.
Let's look at the Figure 3 of the original article. The circular plate (or the artificial tongue) was elevated in the same velocity profile as cat's lapping tongue. We could see that as the circular plate elevates, it produces a water column. The column is narrower near the circular plate, and ultimately collapses into one point at the height Zp. The column then detaches from the plate and falls down due to the action of gravity.
Now let's try to formulate the system. (The derivation could be also found in the original article and its supplementary materials.) Consider under the gravity g, a circular plate with radius R is going to lap the water with density ρ. The plate elevates to height Z(t) after time t. At time t, for a horizontal section of water with height (Z(t) - z), there is a pressure difference from the water surface with magnitude ρg(Z(t)-z). Such pressure difference would drive the motion of water, and its magnitude of kinetic energy density is about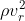 . We could therefore estimate the inward radial speed of water to be
. We could therefore estimate the inward radial speed of water to be -z)}) . The highest height the circular plate could elevate is H.
. The highest height the circular plate could elevate is H.
In the real world, dZ/dt is not a constant, which creates a large obstacle for as to write down how Z depends on t. However, for simplicity, we assume that&space;=&space;U_{max}t) , where Umax is the maximum elevating speed of the plate. With the aid of such simplification, we could estimate that the time required for a horizontal section of water column which is below the disk with distance z would totally take time
, where Umax is the maximum elevating speed of the plate. With the aid of such simplification, we could estimate that the time required for a horizontal section of water column which is below the disk with distance z would totally take time 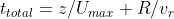 to disappear. The former term (z/U) is the time required for its creation while the latter term (R/v) is the time required for its extinction after its creation.
to disappear. The former term (z/U) is the time required for its creation while the latter term (R/v) is the time required for its extinction after its creation.
To find the height where the water column collapse, or Zp, we could simply partially differentiate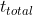 with respect to z。After some simple calculation, we would find that
with respect to z。After some simple calculation, we would find that
in which Fr is a dimensionless quantity called Froude number. It could be defined as
which basically describe the seesaw battle between the speed of plate elevation and the speed gained from gravitational force.
We could also estimate the maximum volume of the water column. Consider again the horizontal section of water column which is below the disk with distance z. The time requires for its creation is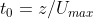 . After another
. After another -z)/U_{max}) , the horizontal section would collapse inward due to the inward radial speed of water, which was estimated previously to be
, the horizontal section would collapse inward due to the inward radial speed of water, which was estimated previously to be -z)}=\sqrt{gU_{max}\Delta&space;t}) . Therefore we could estimate the change in radius to be
. Therefore we could estimate the change in radius to be
And we could therefore estimate the volume of water column to be
After simple calculation we will get
And the height Z which maximize the volume of water column is 0.83R*Fr^2/3. All these predictions have been validated by the authors of the suggested readings with the artificial tongue model.
From the above discussion, we would also expect that the frequency of lapping should depend on the time required for the water column to collapse. The Froude number of cat's tongue is about 0.4. Therefore Zp/Umax ~ H/Umax, and we could then expect that
The scaling law was also validated by the authors with records from zoo and YouTube videos.
Maybe the next time you see a cat lapping, you could explain the mechanism to your friends. And they may find you super-cool!!
/*---------Divider---------*/
Suggested Reading:
Reis, P. M., Jung, S., Aristoff, J. M., Stocker, R. (2010). How Cats Lap: Water Uptake by Felis catus. Science 330(6008): 1231-1234.
Reference:
[1] Galton, Peter M. (1973). The cheeks of ornithischian dinosaurs. Lethaia 6.1 : 67–89.
In the Chinese version, this was the first article in 3min Biophysics. In this episode, we are going to discuss the physics of how cats drink water. The suggested reading (which is also the original journal article) could be found below. And the Chinese version of this episode could be found in 貓喝水的物理:https://goo.gl/SJIZCM.
/*---------Divider---------*/
Most mammals, including human, could suck in water with the negative pressure produced by the contraction of buccinator muscle. However, the mammals which belongs to the Carnivora cannot simply suck in water as we do, since their buccinator muscles have evolved into U-shaped in order to permit wider opening of their mouth. How do cats drink water efficiently?
With the aids of high-speed imaging, Reis and their colleagues could closely observe how cat "laps" water. They found that during the lapping process, the tongues of cats do not penetrate the water surface. Instead, the tip of tongue touches the water surface and rapidly elevates, which brings up a water column. The cat then close its mouth to ingest the water just have been brought up by its tongue.
However, is that really a physically feasible mechanism to drink water? Does this mechanism impose any limitation on cats? That's what a biophysicist care about. Therefore, Reis and their colleagues made an artificial tongue model to analyze the mechanism of lapping water and used dimensional analysis to make prediction about how the lapping frequency varies with animal sizes.
Artificial tongue model of lapping. The original figure came from the figure 3 of Reis, P. M., Jung, S., Aristoff, J. M., Stocker, R. (2010). How Cats Lap: Water Uptake by Felis catus. Science 330(6008): 1231-1234.
Let's look at the Figure 3 of the original article. The circular plate (or the artificial tongue) was elevated in the same velocity profile as cat's lapping tongue. We could see that as the circular plate elevates, it produces a water column. The column is narrower near the circular plate, and ultimately collapses into one point at the height Zp. The column then detaches from the plate and falls down due to the action of gravity.
Now let's try to formulate the system. (The derivation could be also found in the original article and its supplementary materials.) Consider under the gravity g, a circular plate with radius R is going to lap the water with density ρ. The plate elevates to height Z(t) after time t. At time t, for a horizontal section of water with height (Z(t) - z), there is a pressure difference from the water surface with magnitude ρg(Z(t)-z). Such pressure difference would drive the motion of water, and its magnitude of kinetic energy density is about
In the real world, dZ/dt is not a constant, which creates a large obstacle for as to write down how Z depends on t. However, for simplicity, we assume that
To find the height where the water column collapse, or Zp, we could simply partially differentiate
in which Fr is a dimensionless quantity called Froude number. It could be defined as
which basically describe the seesaw battle between the speed of plate elevation and the speed gained from gravitational force.
We could also estimate the maximum volume of the water column. Consider again the horizontal section of water column which is below the disk with distance z. The time requires for its creation is
And we could therefore estimate the volume of water column to be
After simple calculation we will get
And the height Z which maximize the volume of water column is 0.83R*Fr^2/3. All these predictions have been validated by the authors of the suggested readings with the artificial tongue model.
From the above discussion, we would also expect that the frequency of lapping should depend on the time required for the water column to collapse. The Froude number of cat's tongue is about 0.4. Therefore Zp/Umax ~ H/Umax, and we could then expect that
The scaling law was also validated by the authors with records from zoo and YouTube videos.
Maybe the next time you see a cat lapping, you could explain the mechanism to your friends. And they may find you super-cool!!
/*---------Divider---------*/
Suggested Reading:
Reis, P. M., Jung, S., Aristoff, J. M., Stocker, R. (2010). How Cats Lap: Water Uptake by Felis catus. Science 330(6008): 1231-1234.
Reference:
[1] Galton, Peter M. (1973). The cheeks of ornithischian dinosaurs. Lethaia 6.1 : 67–89.

Comments
Post a Comment