#13 How enzymes propel themselves-III

/*-------------Divider-------------*/

After our discussion about the macroscopic diffusion, or the Fick's law, we will talk about the microscopic formulation of diffusion by Einstein. Einstein started approaching this problem from the perspective of probability and the conservation of probability, or the continuity equation, and ultimately reproduce Fick's law. He solved the diffusion equation and derived a famous equation:

$\left \langle x^2 \right \rangle=2Dt$

/*-------------Divider-------------*/

Derivation of Fick's law from conservation of probability--the microscopic basis of diffusion

We have talked about the diffusion equation governing the foul-smelling molecules in fart. However, we did not talk about the microscopic nature of diffusion. Why should these molecules move around? Or even more basically, are they really moving?

Robert Brown, a botanist, qualitatively recorded the random motion of pollen suspended in water, which was then called Brownian motion. Einstein proposed that the motion of pollen is caused by the collision of pollen with water molecules in 1905, and he formulated the random walk model to explain the observed motion pattern. We could derive Fick's law from this random walk model.

It is always beneficial to start from a 1 dimensional system if the 3 dimensional one looks too formidable. Einstein started from the concept of probability. What is the probability density p(x,t) to find a particle in location x at time t ? Assume the particle in x have probability kΔt to move to the left or right and probability (1-2kΔt) to stay in x every time Δt. Assume the stride length of the particle equals a.

Consider the net probability flux j between x and x+a, it could be written:

$j = \frac{ap(x,t)k\Delta t - ap(x+a, t)k\Delta t}{\Delta t}$

After Taylor expansion of p(x+a, t) and some arithmetics, it becomes:

$j = -a^2k\frac{\partial p}{\partial x}$

If we define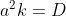 $a^2k=D$ , Fick's first law reappears.

Aside from these, we could written the following equation according to the conservation of probability:

$p(x, t+\Delta t) = (1-2k\Delta t)p(x, t) + (k\Delta t)p(x-a, t) + (k\Delta t)p(x+a, t)$

The 3 terms represent "not moving," "move from the left," and "move from the right", respectively. Assume a and Δt small enough, we could simplify the above equation using Taylor expansion:

$\\ p(x, t+\Delta t) \approx p(x, t) + \Delta t\frac{\partial p(x,t)}{\partial t}\\ p(x\pm a,t) \approx p(x,t) \pm a\frac{\partial p(x,t)}{\partial x} + \frac{a^2}{2}\frac{\partial^2 p}{\partial x^2}$

After simple arithmetics, the conservation of probability now reads

$\frac{\partial p}{\partial t}=(a^2k)\frac{\partial^2 p}{\partial x^2}$

It will become Fick's second law if we again define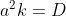 $a^2k=D$ . In 3 dimensional form, the above equation becomes

$\frac{\partial p}{\partial t}=D\triangledown ^2p$

Diffusion with convection

We assume the probability of moving to left and to right the same. What if these 2 probability are different? It may happen if your classmate use a hand fan to avoid smelling your fart. Assume the probability of moving to the right rΔt and moving to the left sΔt in time Δt. The conservation of probability now reads:

$p(x, t+\Delta t) = (1-(r+s)\Delta t)p(x, t) + (r\Delta t)p(x-a, t) + (s\Delta t)p(x+a, t)$

Again we use Taylor expansion and we will get:

$\frac{\partial p}{\partial t}=-(r-s)a\frac{\partial p}{\partial x}+(r+s)\frac{a^2}{2}\frac{\partial^2 p}{\partial x^2}$

Define (r-s)*a=v, or drift velocity. Define (r+s)*(a^2/2) = D. We will get the Smoluchowski equation:

$\frac{\partial p}{\partial t}=-v\frac{\partial p}{\partial x}+D\frac{\partial^2 p}{\partial x^2}$

The solution of Diffusion equation with delta function initial condition

We will then try to solve the diffusion equation without convection term with delta function initial condition. Assume all molecules initially concentrated in x=0. This distribution pattern could be expressed as a delta function δ(x). So our problem about the diffusion of your fart now becomes

$\frac{\partial p}{\partial t}=D\frac{\partial^2 p}{\partial x^2},\quad p(x,0)=\delta(x),\quad p(\pm \infty,t)=0,\quad p(x,t)=?$

The delta function looks troublesome and it is actually a special function. For more information, please read about our episode #50 (http://biophys3min.blogspot.tw/2016/06/50diracdeltafunction.html). We would like to transform it into something benign, so we perform Fourier transform on the above equation:

$\\ \frac{1}{\sqrt{2\pi}}\int_{-\infty}^{\infty}\frac{\partial p(x,t)}{\partial t}e^{-i\omega x}\textup{d}x = \frac{D}{2\pi}\int_{-\infty}^{\infty}\frac{\partial^2 p(x,t)}{\partial x^2}e^{-i\omega x}\textup{d}x\\ \frac{1}{\sqrt{2\pi}}\int_{-\infty}^{\infty}p(x,0)e^{-i\omega x}\textup{d}x = \frac{1}{\sqrt{2\pi}}\int_{-\infty}^{\infty}\delta(x)e^{-i\omega x}\textup{d}x$

Assume that

$\frac{1}{\sqrt{2\pi}}\int_{-\infty}^{\infty}p(x,t)e^{-i\omega x}\textup{d}x = F(\omega,t)$

The above equation then becomes (using integration by parts)

$\\ \frac{\partial F(\omega, t)}{\partial t} = -D\omega^2F(\omega,t)\\ F(\omega,0)=\frac{1}{\sqrt{2\pi}}$

This is a simple ODE with solution

$F(\omega, t) = \frac{1}{\sqrt{2\pi}}e^{-D\omega^2t}$

We will now perform inverse Fourier transform on F and we will get (using Gaussian integral)

$p(x,t)=\frac{1}{\sqrt{2\pi}}\int_{-\infty}^{\infty}\frac{1}{\sqrt{2\pi}}e^{-D\omega^2t}e^{i\omega x}\textup{d}\omega = \frac{1}{\sqrt{4\pi D t}}e^{\frac{-x^2}{4Dt}}$

Now we get the probability density of the molecules in x at time t. To estimate how far the particles diffuse, since the probability density function is an even function with respect to x, it is reasonable to calculate the expectation value of x^2, or <x^2>:

$\left \langle x^2 \right \rangle = \int_{-\infty}^{\infty} x^2p(x)\textup{d}x =\frac{1}{\sqrt{4\pi D t}}\int_{-\infty}^{\infty}x^2e^{\frac{-x^2}{4Dt}}\textup{d}x = 2Dt$

or <x^2> = 2Dt. It implies the root-mean-square distance of diffusion is proportional to the square root of time.

#biophysics #3minBiophysics #生物物理 #三分鐘生物物理
#diffusion #Einstein formulation

Three Minute Biophysics

Search This Blog

Featured Post

#77 Brownian Carnot engine-I 微觀卡諾引擎-I