- Get link
- X
- Other Apps
Featured Post
- Get link
- X
- Other Apps
/*-----------Divider-----------*/
We have previously discusses the Langevin equation in episode 14 (http://biophys3min.blogspot.tw/2016/09/14-how-enzymes-propel-themselves-iv.html). Due to its great importance, we will discuss more properties of Langevin equation in this episode.
我們在第14集曾經討論過朗之萬方程,因為他的重要性,所以我們在這幾集裡面要更深入介紹他的一些相關性質。
我們已經說過朗之萬方程式其實就是在牛頓第二定律中,把力變成隨機力:
or written in terms of velocity
如果把他寫成速度的方程式,他就變成
in which F(t) follows
而我們的隨機力遵從白雜訊的性質
For a one dimensional system and a system satisfying equipartition theorem, the above equation implies
對一個一維且遵從能量均分定理的系統而言,上面的方程式可以直接導出下面的結論
which we have derived in episode 14. However, we skipped the problem of the magnitude of noise by multiplying the equation by x and using the fact that
這我們在第14集有說明過了。不過我們那時候採用了一點偷工減料的方式,把方程式兩邊同乘x, 然後利用下面的事實,規避掉雜訊的大小到底有多大的問題。
Today, we will start from discussing the magnitude of noise.
這不是一個長久之計,尤其是當你想要做模擬的時候,你必須知道雜訊的大小,所以我們今天就從雜訊的大小開始。
我們來看看以速度表示的朗之萬方程
Its solution is clear-cut
上面這個ODE的答案非常簡單且直白
This equation could be solved by numerical method, or we could switch to the equivalent Fokker-Planck equation. Both of them will be discussed in the following episodes.
實務上我們可以用數值方法得到上面的答案,也可以把朗之萬方程轉成他等效的福克-普朗克方程,而我們在後面兩種方法都會講解。
Consider the average of square of velocity:
現在考慮一下速度平方的平均應該有多大:
v(t)&space;\right&space;\rangle=v(0)v(0)e^{-2\zeta&space;t/m}+2e^{-2\zeta&space;t/m}\int_{0}^{t}\frac{v(0)\left&space;\langle&space;F(t')&space;\right&space;\rangle}{m}e^{\zeta&space;t'/m}\textup{d}t'+e^{-2\zeta&space;t/m}\int_{0}^{t}\textup{d}t''\int_{0}^{t}\textup{d}t'\frac{\left&space;\langle&space;F(t')F(t'')&space;\right&space;\rangle}{m^2}e^{\zeta(t'+t'')/m})
From the definition of white noise, it is easily to show that
看起來真的挺複雜的,不過如果我們套用白雜訊的定義化簡一下,他就會變得蠻簡單的
Since for large t, the average should be equal to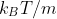 , which means the magnitude of noise should be
, which means the magnitude of noise should be
因為當時間足夠長的時候,上面的平均值必須等於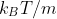 。這代表雜訊的強度必須等於
。這代表雜訊的強度必須等於
對於生物物理學家而言, 過阻尼版本的朗之萬方程其實比朗之萬方程更常使用,因為我們感興趣的分子、蛋白質是處在一個低雷諾數的環境。在雷諾數低的情況下,流體運動為層流,慣性的效應可以忽略。因此我們拿出原本的朗之萬方程,移除慣性的項之後,在原本的隨機力之外,額外加上一個保守力,我們就寫出了過阻尼朗之萬方程:
It is important to recognize that this simplification would render the transient dynamics of the system incorrectly.
有件很重要的事情需要注意的是,當我們使用過阻尼朗之萬方程時,我們得到的結論在長時間尺度下是正確的,但在過渡期間的答案是錯誤的。
The overdamped Langevin equation would give rise to the Einstein relation if we take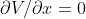
如果我們把保守力的項移除,那過阻尼朗之萬方程就會變成random walk model,而我們就可以得到前面已經推過好幾次的Einstein relation:
The overdamped Langevin equation would be used heavily in the following episodes.
這個方程式我們後面還會頻繁的使用他喔!
/*-----------Divider-----------*/
Reference:
Bialek, W. 2012. Biophysics: Searching for Principles. The US: Princeton University Press.
We have previously discusses the Langevin equation in episode 14 (http://biophys3min.blogspot.tw/2016/09/14-how-enzymes-propel-themselves-iv.html). Due to its great importance, we will discuss more properties of Langevin equation in this episode.
我們在第14集曾經討論過朗之萬方程,因為他的重要性,所以我們在這幾集裡面要更深入介紹他的一些相關性質。
Review on Episode 14 簡短的回顧
We have previously introduced the Langevin equation, which is basically a stochastic generalization of the Newton's second law:我們已經說過朗之萬方程式其實就是在牛頓第二定律中,把力變成隨機力:
or written in terms of velocity
如果把他寫成速度的方程式,他就變成
in which F(t) follows
而我們的隨機力遵從白雜訊的性質
For a one dimensional system and a system satisfying equipartition theorem, the above equation implies
對一個一維且遵從能量均分定理的系統而言,上面的方程式可以直接導出下面的結論
which we have derived in episode 14. However, we skipped the problem of the magnitude of noise by multiplying the equation by x and using the fact that
這我們在第14集有說明過了。不過我們那時候採用了一點偷工減料的方式,把方程式兩邊同乘x, 然後利用下面的事實,規避掉雜訊的大小到底有多大的問題。
Today, we will start from discussing the magnitude of noise.
這不是一個長久之計,尤其是當你想要做模擬的時候,你必須知道雜訊的大小,所以我們今天就從雜訊的大小開始。
Magnitude of Noise 雜訊的大小
Let's start from the velocity form of Langevin equation:我們來看看以速度表示的朗之萬方程
Its solution is clear-cut
上面這個ODE的答案非常簡單且直白
This equation could be solved by numerical method, or we could switch to the equivalent Fokker-Planck equation. Both of them will be discussed in the following episodes.
實務上我們可以用數值方法得到上面的答案,也可以把朗之萬方程轉成他等效的福克-普朗克方程,而我們在後面兩種方法都會講解。
Consider the average of square of velocity:
現在考慮一下速度平方的平均應該有多大:
From the definition of white noise, it is easily to show that
看起來真的挺複雜的,不過如果我們套用白雜訊的定義化簡一下,他就會變得蠻簡單的
Since for large t, the average should be equal to
因為當時間足夠長的時候,上面的平均值必須等於
Overdamped Langevin Equation 過阻尼朗之萬方程
For a biophysicist, we often consider the overdamped Langevin equation because the system we are interested in (molecules and proteins in water) is a small-Reynold number system in which the inertial effect is negligible. The Langevin equation could then be written in a form with a potential V but without inertial term:對於生物物理學家而言, 過阻尼版本的朗之萬方程其實比朗之萬方程更常使用,因為我們感興趣的分子、蛋白質是處在一個低雷諾數的環境。在雷諾數低的情況下,流體運動為層流,慣性的效應可以忽略。因此我們拿出原本的朗之萬方程,移除慣性的項之後,在原本的隨機力之外,額外加上一個保守力,我們就寫出了過阻尼朗之萬方程:
It is important to recognize that this simplification would render the transient dynamics of the system incorrectly.
有件很重要的事情需要注意的是,當我們使用過阻尼朗之萬方程時,我們得到的結論在長時間尺度下是正確的,但在過渡期間的答案是錯誤的。
The overdamped Langevin equation would give rise to the Einstein relation if we take
如果我們把保守力的項移除,那過阻尼朗之萬方程就會變成random walk model,而我們就可以得到前面已經推過好幾次的Einstein relation:
The overdamped Langevin equation would be used heavily in the following episodes.
這個方程式我們後面還會頻繁的使用他喔!
/*-----------Divider-----------*/
Reference:
Bialek, W. 2012. Biophysics: Searching for Principles. The US: Princeton University Press.
- Get link
- X
- Other Apps
Comments
Post a Comment