- Get link
- X
- Other Apps
Featured Post
- Get link
- X
- Other Apps
/*-------------Divider-------------*/
Before reading, let's watch the following video (start from 0:48)
https://www.youtube.com/watch?v=45yabrnryXk
/*-------------Divider-------------*/
Walking on water is a fascinating trick that suggests divine power in folktales and Bible stories. Although we can't walk on water under ordinary settings, basilisk lizards (Basiliscus basiliscus) are capable of doing so. Why we can't walk on water as the lizards do?
Glasheen & McMahon believed that basilisk lizards walk on water through 3 processes: slap, stroke and protraction. The first 2 steps would generate the counter force to support its weight. In order to find out the underlying physics mechanism, they used circular disc and then the model of lizard's foot for impact experiment on water surfaces, and compare it to the observed results from real lizards.
Let's first consider the impulse generated from slap. As the lizard slap the surface with its foot of mass m0, part of its momentum would be transferred to the water. The mass of water that would be accelerated is called virtual mass,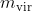 . Assume that the foot is decelerated by Δu during the slap and its final velocity becomes
. Assume that the foot is decelerated by Δu during the slap and its final velocity becomes 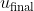 , and the water with virtual mass would be accelerated to
, and the water with virtual mass would be accelerated to 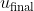 . From the conservation of momentum,
. From the conservation of momentum, 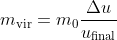 , and the impulse given from water to the foot of lizard would be
, and the impulse given from water to the foot of lizard would be 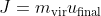 . According to the experimental results, a circular disc with radius r would accelerate water with virtual mass
. According to the experimental results, a circular disc with radius r would accelerate water with virtual mass 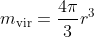 , and we could estimate the virtual mass associated with the model of lizard's foot.
, and we could estimate the virtual mass associated with the model of lizard's foot.
And then we try to estimate the impetus generated from each stroke. As the foot strike into the water, the water is displaced and brings air column down below the water surface. To accelerate the water, the foot of lizard must generate forces. From the conservation of energy, a foot with area S striking into the water with speed u in order to form an air column with depth h must generate force that measures
 , in which C is an constant associated to the shape of foot, or the so called drag coefficient. Since every force is accompanied by a reaction force D, in this case the drag force. We could integrate the vertical component of drag force with respect to time to get the impetus.
, in which C is an constant associated to the shape of foot, or the so called drag coefficient. Since every force is accompanied by a reaction force D, in this case the drag force. We could integrate the vertical component of drag force with respect to time to get the impetus.
Assume the time interval between 2 consecutive strokes is T, the mass of lizard M. The impetus generated from slaps and strokes must balance out the impetus from gravity. Therefore,
 We could evaluate the model after we get the above equation. The authors experimentally measured the virtual mass and drag coefficient of each size of lizard foot, and calculated the impetus from observed stroke velocity and time profile. On average, the impetus generated from slaps and strokes is the 1.02 times of that generated from gravity. Furthermore, we could differentiate the contribution from slaps and strokes from this model.
We could evaluate the model after we get the above equation. The authors experimentally measured the virtual mass and drag coefficient of each size of lizard foot, and calculated the impetus from observed stroke velocity and time profile. On average, the impetus generated from slaps and strokes is the 1.02 times of that generated from gravity. Furthermore, we could differentiate the contribution from slaps and strokes from this model.
Walking on water experiences much less drag forces than swimming, and thus an robot designed for that would perform much more efficiently. Besides, some physicists inspired by this research tried to find out the conditions which allow human to walk on water. If you are interested, enjoy our reference articles.
/*-------------Divider-------------*/
Suggested Readings:
1. J. W. Glasheen & T. A. McMahon. A hydrodynamic model of locomotion in the Basilisk Lizard. Nature 380(28): 340-342. (1996).
2. J. W. Glasheen & T. A. McMahon. Size-dependence of water-running ability in Basilisk Lizards (Basiliscus basiliscus). The Journal of Experimental Biology 199, 2611–2618 (1996).
3. J. W. Glasheen & T. A. McMahon. Vertical water entry of disks at low Froude Numbers. Physics of Fluids 8, 2078–2083. (1996).
Reference:
1. A. E. Minetti, Y. P. Ivanenko, G. Cappellini, N. Dominici, F. Lacquaniti. Humans Running in Place on Water at Simulated Reduced Gravity. PLoS One 7(7): 37300. (2012).
#biophysics #3minBiophysics #生物物理 #三分鐘生物物理
#lizard #fluid #mechanics #locomotion
Before reading, let's watch the following video (start from 0:48)
https://www.youtube.com/watch?v=45yabrnryXk
/*-------------Divider-------------*/
Walking on water is a fascinating trick that suggests divine power in folktales and Bible stories. Although we can't walk on water under ordinary settings, basilisk lizards (Basiliscus basiliscus) are capable of doing so. Why we can't walk on water as the lizards do?
Glasheen & McMahon believed that basilisk lizards walk on water through 3 processes: slap, stroke and protraction. The first 2 steps would generate the counter force to support its weight. In order to find out the underlying physics mechanism, they used circular disc and then the model of lizard's foot for impact experiment on water surfaces, and compare it to the observed results from real lizards.
Let's first consider the impulse generated from slap. As the lizard slap the surface with its foot of mass m0, part of its momentum would be transferred to the water. The mass of water that would be accelerated is called virtual mass,
And then we try to estimate the impetus generated from each stroke. As the foot strike into the water, the water is displaced and brings air column down below the water surface. To accelerate the water, the foot of lizard must generate forces. From the conservation of energy, a foot with area S striking into the water with speed u in order to form an air column with depth h must generate force that measures
Assume the time interval between 2 consecutive strokes is T, the mass of lizard M. The impetus generated from slaps and strokes must balance out the impetus from gravity. Therefore,
Walking on water experiences much less drag forces than swimming, and thus an robot designed for that would perform much more efficiently. Besides, some physicists inspired by this research tried to find out the conditions which allow human to walk on water. If you are interested, enjoy our reference articles.
/*-------------Divider-------------*/
Suggested Readings:
1. J. W. Glasheen & T. A. McMahon. A hydrodynamic model of locomotion in the Basilisk Lizard. Nature 380(28): 340-342. (1996).
2. J. W. Glasheen & T. A. McMahon. Size-dependence of water-running ability in Basilisk Lizards (Basiliscus basiliscus). The Journal of Experimental Biology 199, 2611–2618 (1996).
3. J. W. Glasheen & T. A. McMahon. Vertical water entry of disks at low Froude Numbers. Physics of Fluids 8, 2078–2083. (1996).
Reference:
1. A. E. Minetti, Y. P. Ivanenko, G. Cappellini, N. Dominici, F. Lacquaniti. Humans Running in Place on Water at Simulated Reduced Gravity. PLoS One 7(7): 37300. (2012).
#biophysics #3minBiophysics #生物物理 #三分鐘生物物理
#lizard #fluid #mechanics #locomotion
Comments
Post a Comment