- Get link
- Other Apps
/
After we explained the observed scaling law, today we will talk more about the energy budget related to removing water. Even the animals shake off most of the water, some residual will still stay between hairs. Assume the hairs to be perpendicular to the skin surface, and those hairs are too hard to be bent. Assume the distance between 2 hairs d, the surface tension of water σ, the density of water
ρ, the contact angle between hair and water θ. According to the principle of capillary action,the height of water column that could be kept between 2 hairs are
if we define capillary length, Lc = sqrt(σ/ρg).
However, hairs are susceptible to bending most of the time, and such bending would cost energy, which is done by the surface tension of water. Assume the full length of hair L, the length of the part that is wet L_wet, the length of the part that is dry L_dry. Besides, the part that is wet would adhere to each other like the following figure.
Assume the diameter of hair b. The energy contributed from surface tension could be calculated as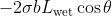
. What about the energy from bending? Recall that we have briefly discussed some material mechanics in [#3 Scaling law of locomotion-II]. Given the area moment of inertia of hairs I, the Young's modulus of hairs E, the curvature after bending κ, the total energy required could be calculated as
^2\textup{d}s "W = \frac{EI}{2}\int_{0}^{L}\kappa(s)^2\textup{d}s")
We have also talked about a way to estimate the curvature in [#9 The optimal concentration of nectar-IV]. Since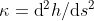 
, given the lateral displacement of hairs d, the length of the part that is bent L_dry, the curvature could be estimated as
Thus, the energy of bending would be
Finally, the total energy would be
\cos\theta+&space;3EId^2/L_{\textup{dry}}^3 "-2\sigma b(L-L_{\textup{dry}})\cos\theta+ 3EId^2/L_{\textup{dry}}^3")
Differentiate the total energy with respect to L_dry and we would know that the energy is minimized when
^{1/4} "L_{\textup{dry}} = (\frac{9}{2}d^2\frac{EI}{\sigma b \cos\theta})^{1/4}")
From the above discussion, the height of water columns between hairs is initially
^{1/4} "H_{\textup{init}}=L-(\frac{9}{2}d^2\frac{EI}{\sigma b \cos\theta})^{1/4}")
Then we could calculate the remaining moisture content (RMC) as
in which D is a correction term accounting for the water that is absorbed into keratin and impossible to be shaken off. The constant D was estimated to be about 30% by isolated animal fur. Experimentally observed RMC after shaking was also about 30%. Which means the frequencies of shaking are adjusted to make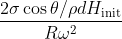 
nearly 0.
Last but not least, the authors compared the energy required to shake off water and that required to wait them evaporate. It was estimated to be only about 1/1000 to 1/10000 times the energy required to wait them evaporate. The benefit comes from shaking water off is then obvious.
/
Suggested Reading：
1. A. K. Dickerson, Z. G. Mills and D. L. Hu. Wet mammals shake at tuned frequencies to dry. J. R. Soc. Interface 13(116): 3208-3218. (2012).
2. J. Bico, B. Roman, L. Moulin, A. Boudaoud. Elastocapillary coalescence in wet hair. Nature 432(9): 690. (2014)
#biophysics #3minBiophysics #生物物理 #三分鐘生物物理
#fluid #mechanics #surface #tension #scaling law
After we explained the observed scaling law, today we will talk more about the energy budget related to removing water. Even the animals shake off most of the water, some residual will still stay between hairs. Assume the hairs to be perpendicular to the skin surface, and those hairs are too hard to be bent. Assume the distance between 2 hairs d, the surface tension of water σ, the density of water
ρ, the contact angle between hair and water θ. According to the principle of capillary action,the height of water column that could be kept between 2 hairs are
This is called Jurin’s law. We could rewrite the above formula into
However, hairs are susceptible to bending most of the time, and such bending would cost energy, which is done by the surface tension of water. Assume the full length of hair L, the length of the part that is wet L_wet, the length of the part that is dry L_dry. Besides, the part that is wet would adhere to each other like the following figure.
ref: Nature 432, 690 (9 December 2004) | doi:10.1038/432690a
If we could calculate the energy contribution from surface tension and the bending of hair, then we could predict L_wet & L_dAssume the diameter of hair b. The energy contributed from surface tension could be calculated as
Differentiate the total energy with respect to L_dry and we would know that the energy is minimized when
From the above discussion, the height of water columns between hairs is initially
while the final height of water columns between hairs after animal's shaking would be
Last but not least, the authors compared the energy required to shake off water and that required to wait them evaporate. It was estimated to be only about 1/1000 to 1/10000 times the energy required to wait them evaporate. The benefit comes from shaking water off is then obvious.
/
Suggested Reading：
1. A. K. Dickerson, Z. G. Mills and D. L. Hu. Wet mammals shake at tuned frequencies to dry. J. R. Soc. Interface 13(116): 3208-3218. (2012).
2. J. Bico, B. Roman, L. Moulin, A. Boudaoud. Elastocapillary coalescence in wet hair. Nature 432(9): 690. (2014)
#biophysics #3minBiophysics #生物物理 #三分鐘生物物理
#fluid #mechanics #surface #tension #scaling law
Comments
Post a Comment