#26 Fundamentals: Blasius boundary layer

/*-------------Divider-------------*/
Have you ever been entrapped in a swamp or at least seen it in movies? It is a low Reynolds number condition when you move in a highly viscous fluid. It is the viscous forces that not only prevent you from moving but also drag the surrounding fluid to go with you. How much fluid do we drag with us? We could get some hints from Navier-Stokes equation.

In our previous episode (http://biophys3min.blogspot.tw/2016/03/25navier-stokes-equation.html) we introduced Navier-Stokes equation. Today we will apply it to a simplified system. This is a fluid-filled two-dimensional system with a boundary on the x-axis. For a fluid element, its velocity equals to u and v in x and y directions, respectively. Water near the boundary moves slower while that far from the boundary moves with a constant velocity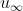 . We would like to know how thick the transition zone from u=0 to u = 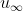is (denoted as δ here).

We will first see how compressibility restricts fluid motion. Consider a fluid element

The left border of the fluid element at time t has location x and velocity u(x) while the right border of it has location x+Δx and velocity u(x+Δx). After time Δt, the location of the left and right border would become x+ u(x)Δt and x+Δx+ u(x+Δx)Δt, respectively. This means the fluid element could widen itself as time goes. If we consider all 3 dimension, it means the volume of the fluid element could change from ΔxΔyΔz to

 

If that volume change is allowable, we are discussing a compressible fluid. If we are discussing something incompressible, like water, the divergence of the flow field has to be 0.

So let's get back to our 2 dimensional transition zone problem. The incompressibiliy imposes the following restriction:

 

To solve this we need other equations, so we refer to Navier-Stokes equation. Since the flow field is in steady state and the body forces is relatively negligible here, Navier-Stokes equation could be simplified as follow:

Three equations in total.

The above 3 equations look troublesome. We are not better at solving these ugly stuff, either, so we should try to eliminate some terms. Since our system extends along x till infinity and the velocity is mainly toward x direction, we could reasonably assume that

 

After these tricky steps our original equations now become

 

It looks much better right now!

But that is not the end of our simplification. Since 0 = - ∂p/∂y (the 3rd equation above), p only depends on x, or p = p(x). However, for fluid that is far from the boundary, the velocity of fluid elements equals to u_∞, which does not depend on x. Therefore the pressure p must not vary with x. This means the pressure is a constant in our system. The 3 equations above now only left 2.

 
So now it is time to derive our δ, the thickness of transition zone. However, the explicit solution is still a little bit difficult. We will therefore approximate it with dimension analysis. If we could define some "characteristic length" in x direction, the above equation would be:

From this we could derive that (Re = Reynold number = ρuL/η)

This is left for our readers as a small practice.

So then we could now estimate how much water would be dragged by a man in a swimming pool. Assume the height of the man 2m, swimming speed 1m/s, density of water 1000kg/m^3, viscosity of water 10^(-3) Pa‧s. It could be estimated that

It's quite thin, isn't it? From this we could estimate the drag forces derived from viscosity. Assume the surface area of the man 2m^2. The drag forces from viscosity would be:

Much smaller than our weight 600N. The drag forces we encounter in water mainly comes from pressure drag (that we have discussed in #19 The possibility of walking on water). However, if we change the medium into honey (viscosity ~ 10 Pa‧s, density 1400kg/m^3), the same speed would cause viscosity drag as large as 200N, and that would be non-negligible.

#biophysics #3minBiophysics #生物物理 #三分鐘生物物理 #常識集 #fundamentals #Blasius boundary layer #fluid #mechanics #viscosity