- Get link
- X
- Other Apps
Featured Post
- Get link
- X
- Other Apps
/*-------------Divider-------------*/
Please finish reading episode 6 before reading this episode. Today we are going to talk about the capillary suction.
Suggested Video:Please finish reading episode 6 before reading this episode. Today we are going to talk about the capillary suction.
https://www.youtube.com/watch?v=QYoYQAbPXbU
/*------------ Divider -------------*/
In previous episode, we have written down
the equation governing the nectar with density ρ, viscosity μ and mean
flow velocity u in a mouthpiece with
length L, and inner radius a
according to Newton’s second law:
For capillary sucker such as hummingbirds,
they lack the ability to produce negative pressure (recently there are some
researches finding against this hypothesis and we will talk about it later), so
the pressure force term = 0. However, there is an extremely narrow tunnel on
their tongue which allows fluid to arise by capillary flow. Assume the contact
angle between nectar and tongue θ,
and the surface tension of nectar σ,
the original equation now reads:
And we use the same reasoning
to discard the terms considering inertial force and gravitational force as we
did in previous episode. The equation now reads
Now here is the problem. The
capillary sucker must retract their tongue after the whole narrow tunnel is
filled with nectar in order to permit the next filling. (Please refer to the
suggested video to observe this process.) Namely the height of liquid column is
a function of time, or h=h(t). And since u=h’(t), the above equation could now
be written as
With the initial condition h(0)=0, it is easy to solve (using hh’ = (0.5h^2)’) h(t)
Now let’s consider the
average volumetric flow rate Q.
Assume the time required to fill up the narrow tunnel on the tongue T, and the time required for tongue
retraction and re-protrusion T0. The
average volumetric flow rate Q could
be calculated as
According to previous
experiments, (T)^0.5 / (T+T0) does not depend on viscosity. Therefore we now
know the power law between average volumetric flow rate and viscosity is
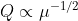
Which is the same as the
active sucker and is supported by experiments.
Someone may have noticed that
we automatically neglect the effect of capillary flow in the governing equation
of active sucker. This could be readily justified by calculation the ratio
between 2 forces:
}&space;=&space;\frac{2\sigma&space;\cos\theta}{\Delta&space;Pa}&space;\sim&space;\frac{\sigma}{\Delta&space;Pa})
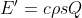
^{1/2})
That is to say, the greater
the inner radius, the smaller the contribution from capillary forces. The
surface tension of water is about 70mN/m, the negative pressure generated by
butterflies is about 10kPa, and the inner radius of the mouthpiece of
butterflies is 100μm. The above ratio is about 0.1 and is therefore negligible.
Nonetheless, recent
literatures (see reference) suggested that hummingbirds could generate negative
pressure by actively changing the shape of the narrow tunnels in their tongues.
However, both hypothesis yield the power law Q ∝μ^(-1/2) and is therefore not differentiable with this approach.
Besides, what truly matters
for creatures is the energy flow rate rather than the volumetric flow rate. Assume
the energy density of sugar c,
density of nectar ρ, and the sugar
concentration s. It is readily to
show that
Previous experiments show
that the density of nectar varies negligibly with the concentration of sugar. We
could therefore write down
With the experimental results
of μ(s), the researchers found that the optimal nectar concentration is about
30% ~ 40%.
In the next episode, we will
discuss the physics of viscous dipper. Stay tuned!
/*------------ Divider
-------------*/
Suggested reading:
Suggested reading:
Kim, W., Gilet, T., and Bush,
J. W. M. (2011). Optimal concentrations in nectar feeding. PNAS 108(40):
16618-16621.
Reference:
Rico-Guevara, A., Fan, T. H.
and Rubega, M. A. (2015). Hummingbird tongues are elastic micropumps. Proc. R. Soc. B 282(1813).
#biophysics #3minBiophysics #生物物理 #三分鐘生物物理
#fluid #mechanics #scaling law #hummingbird
#fluid #mechanics #scaling law #hummingbird
- Get link
- X
- Other Apps
Comments
Post a Comment