- Get link
- X
- Other Apps
Featured Post
- Get link
- X
- Other Apps
Today we will discuss the computer simulation of Langevin equation, implement it to a model system oscillating between 2 potential well, and verify the Arrhenius law for reaction rate constant.
今天我們要來討論朗之萬方程式的電腦模擬,並且把它運用在一個雙位能阱的震盪系統中,並利用這個系統來驗證速率常數與溫度的阿瑞尼士方程式。
Let's start from the overdamped Langevin equation we mentioned previously:
我們首先從上一集提到的過阻尼朗之萬方程式開始:
The equation could be written in a more general form:
這條方程式可以用更普遍的方式表達:
今天我們要來討論朗之萬方程式的電腦模擬,並且把它運用在一個雙位能阱的震盪系統中,並利用這個系統來驗證速率常數與溫度的阿瑞尼士方程式。
Let's start from the overdamped Langevin equation we mentioned previously:
我們首先從上一集提到的過阻尼朗之萬方程式開始:
The equation could be written in a more general form:
這條方程式可以用更普遍的方式表達:
in which ) represents the white noise with magnitude 1:
represents the white noise with magnitude 1:
其中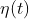 是單位白雜訊:
是單位白雜訊:
Now let's consider the impulse it produces within a small time interval
現在我們來看看在一段很短的時間內,我們的雜訊可以產生的衝量有多少
其中
Now let's consider the impulse it produces within a small time interval
現在我們來看看在一段很短的時間內,我們的雜訊可以產生的衝量有多少
The mean of this tiny impulse is obviously 0. Now let's consider its variance. From the definition of variance, since the mean of the total impulse is 0, we will get
從白雜訊的定義就可以看出來,這個衝量的平均值是零。但他的變異數是多少呢?根據變異數的定義和平均值是0的事實,我們可以寫下
Using the properties of delta function, we will get
再利用到delta函數的特性,我們就可以求出在一段很短時間內,累積衝量的變異數為
which means the impulse in a short time interval is a Gaussian noise. This allows us to write the above stochastic differential equation in discrete form:
這表示在一段很短時間內,隨機力累積的衝量是一個高斯雜訊。知道這件事情之後,我們就可以把原本的隨機微分方程寫成離散的形式:
which could be readily simulated by any programming language.
而這離散的形式就能讓我們用電腦模擬隨機微分方程式。
現在我們要來演示一下朗之萬方程的電腦模擬。我們假設一個有雙位能阱的系統:
The system should oscillate between the 2 potential well. The activation energy is V0. By recording the oscillation pattern under different temperature, we could calculate the rate constant under different temperature and verify the Arrhenius law.
這個系統會在兩個位能阱之間震盪,位能阱之間的活化能大小為 V0。我們可以紀錄在不同溫度下,系統在兩個位能阱之間震盪的情形,求出不同溫度下的反應速率,進而驗證阿瑞尼士方程式。
A test program which simulates the system under temperature 150K would looks like this:
我們先簡單寫一個程式來模擬在150K時系統在兩個位能阱間的情形:
This would yield a figure like this:
畫出來的時間歷程圖長這樣:
By recording the dwelling time in 1 potential well, we could calculate the reaction rate constant easily. However, to reliably calculate the dwelling time, we must remove some noise from the data.
藉由紀錄系統停留在單一側位能阱的時間長短,我們可以求出反應速率。然而,要讓電腦自己計算出停留在一側的時間其實會有困難,必須要把雜訊適當地從我們的數據中移除才行。(讀者也可以試著不這樣做,不過就會發現估計出來的活化能是錯誤的。)
The reaction rate constant estimated is 1.121E+06/s. Now let's try to simulate under different temperature:
在經過適當的移除雜訊後,估計出來的反應速率是 1.121E+06/s。現在我們來試試看在不同溫度下做實驗:
The above program would take about 30 minutes to run. After a long wait, we finally get our reaction rate constant under different temperature. The activation energy could be estimated by linear regression:
上面這個程式大概要花三十分鐘以上才能跑完。在適當的等待之後,我們就能得到在不同溫度下的反應速率了。根據阿瑞尼士方程,把反應速率取對數之後,用線性回歸可以得到活化能:
And the result looks like this:
結果長得像這樣子
The result is compatible to Arrhenius law and the activation energy is estimated to be 1.267E-20, which is close to our setting 1.0E-20. Isn't it amazing?
我們的模擬結果和阿瑞尼士方程非常符合,而且估計出來的活化能1.267E-20 J也和我們設定的1.0E-20 J非常符合。是不是很神奇呢?
從白雜訊的定義就可以看出來,這個衝量的平均值是零。但他的變異數是多少呢?根據變異數的定義和平均值是0的事實,我們可以寫下
Using the properties of delta function, we will get
再利用到delta函數的特性,我們就可以求出在一段很短時間內,累積衝量的變異數為
which means the impulse in a short time interval is a Gaussian noise. This allows us to write the above stochastic differential equation in discrete form:
這表示在一段很短時間內,隨機力累積的衝量是一個高斯雜訊。知道這件事情之後,我們就可以把原本的隨機微分方程寫成離散的形式:
which could be readily simulated by any programming language.
而這離散的形式就能讓我們用電腦模擬隨機微分方程式。
Computer simulation in MATLAB MATLAB電腦模擬
Now we will show how to implement the above discussion in computer simulation. Assume we have a system with a potential well現在我們要來演示一下朗之萬方程的電腦模擬。我們假設一個有雙位能阱的系統:
這個系統會在兩個位能阱之間震盪,位能阱之間的活化能大小為 V0。我們可以紀錄在不同溫度下,系統在兩個位能阱之間震盪的情形,求出不同溫度下的反應速率,進而驗證阿瑞尼士方程式。
A test program which simulates the system under temperature 150K would looks like this:
我們先簡單寫一個程式來模擬在150K時系統在兩個位能阱間的情形:
%% basic setting
r = 5E-9; eta = 8.90E-4;
zeta = 6*pi*eta*r;
kB = 1.38E-23;
syms x;
x0 = 1E-9;
V0 = 1E-20;
V = V0*(1-(x/x0).^2).^2;
F =
matlabFunction(diff(V,x));
V_fun = matlabFunction(V);
%% test simulation
n_sim = 1E7;
x_total = zeros(1, n_sim);
x_total(1)=rand(1,1)*(1E-9);
T =150; A =
sqrt(2*zeta*kB*T*dt);
for i =
2:1:n_sim
x_old = x_total(i-1);
x_total(i) = x_old +
1/zeta*(-dt*F(x_old)+A*randn(1,1));
end
figure;
plot(dt:dt:(n_sim*dt),x_total);
xlabel('time(s)');
ylabel('reaction
coordinate');
This would yield a figure like this:
畫出來的時間歷程圖長這樣:
By recording the dwelling time in 1 potential well, we could calculate the reaction rate constant easily. However, to reliably calculate the dwelling time, we must remove some noise from the data.
藉由紀錄系統停留在單一側位能阱的時間長短,我們可以求出反應速率。然而,要讓電腦自己計算出停留在一側的時間其實會有困難,必須要把雜訊適當地從我們的數據中移除才行。(讀者也可以試著不這樣做,不過就會發現估計出來的活化能是錯誤的。)
HPD = 5000;
coeffMA = ones(1, HPD)/HPD;
avg24hx_total =
filter(coeff24hMA, 1, x_total);
avg_total = filter(coeffMA,
1, x_total);
x_01 = (avg_total>0);
cal_temp = x_01(2:end) -
x_01(1:(end-1));
trans_time_pt =
find(cal_temp);
duration =
(trans_time_pt(2:end) - trans_time_pt(1:(end-1)))*dt;
k_est =
length(duration)/sum(duration);
The reaction rate constant estimated is 1.121E+06/s. Now let's try to simulate under different temperature:
在經過適當的移除雜訊後,估計出來的反應速率是 1.121E+06/s。現在我們來試試看在不同溫度下做實驗:
k_est_total = zeros(1,7);
HPD = 5000;
coeffMA = ones(1, HPD)/HPD;
for T =
900:300:3000
n_sim = 2E7;
n_rec_per = 1;
n_rec = n_sim/n_rec_per;
x_total = zeros(1, n_rec);
x_total(1)=rand(1,1)*(1E-9);
x1 = x_total(1);
A = sqrt(2*zeta*kB*T*dt);
for i = 1:1:n_sim
x_old = x1;
x1 = x_old +
1/zeta*(-dt*F(x_old)+A*randn(1,1));
if mod(i,n_rec_per)==0
x_total(i/n_rec_per + 1) = x1;
end
end
avg_total = filter(coeffMA, 1, x_total);
x_01 = (avg_total>0);
cal_temp = x_01(2:end) - x_01(1:(end-1));
trans_time_pt = find(cal_temp);
duration = (trans_time_pt(2:end) -
trans_time_pt(1:(end-1)))*n_rec_per*dt;
k_est_total((T-600)/300) =
length(duration)/sum(duration);
display(T);
end
The above program would take about 30 minutes to run. After a long wait, we finally get our reaction rate constant under different temperature. The activation energy could be estimated by linear regression:
上面這個程式大概要花三十分鐘以上才能跑完。在適當的等待之後,我們就能得到在不同溫度下的反應速率了。根據阿瑞尼士方程,把反應速率取對數之後,用線性回歸可以得到活化能:
log_k_est_total =
log(k_est_total');
T_total = 1./(900:300:3000);
T_total = T_total';
X = [ones(8,1) T_total ];
format long
b1 = X\log_k_est_total;
yCalc1 = X*b1;
scatter(900:300:3000,k_est_total);
hold on
plot(900:300:3000,exp(yCalc1),'LineWidth',2);
set(gca,'FontSize',14)
xlabel('Temperature(K)','FontWeight','bold','FontSize',14)
ylabel('reaction
rate constant, k(1/s)','FontWeight','bold','FontSize',14)
grid on
display(b1(2)*kB);
And the result looks like this:
結果長得像這樣子
我們的模擬結果和阿瑞尼士方程非常符合,而且估計出來的活化能1.267E-20 J也和我們設定的1.0E-20 J非常符合。是不是很神奇呢?
- Get link
- X
- Other Apps




Comments
Post a Comment